[재능상품] Python을 이용한 CLT (Central Limit Theorem) 시연

정보

업무명 : Python을 이용한 CLT (Central Limit Theorem) 시연
작성자 : 이상호
작성일 : 2020-10-18
설 명 :
수정이력 :

내용

[개요]

안녕하세요? 웹 개발 및 연구 개발을 담당하고 있는 해솔입니다.
다년간 축적된 경험 (기상학 학술 보고서 및 국/영문 학술 논문 게재, 블로그 운영, IT 회사 웹 개발 담당) 및 노하우를 바탕으로 개개인에게 맞춤형 솔루션을 수행할 수 있습니다.
특히 재능 플랫폼 (크몽, 오투잡, 해피캠퍼스, 레포트 월드)에서 누구보다도 경쟁력 있는 가격으로 양질의 서비스를 제공하고 있습니다.
- 아스키 형식의 텍스트 (text) 파일부터 과학자료 형식 (HDF, H5, NetCDF, Grib, Grb) 및 Data Base (DB) 자료까지 다양한 형태의 자료를 이용하여 수집, 전처리, 분석, 시각화해 드립니다.
- 또한 웹 사이트에 대한 정보를 이용한 웹 크롤링 및 그에 따른 엑셀 및 DB 구축도 가능합니다.
- 아울러 기초 통계 (빈도분포, Prired t-test, Wilcoxn 등)에서 지도/비지도 학습을 통한 회귀모형 구축에 이르기 까지 효율적인 통계 정보를 제공합니다.
- 최근 대한민국의 후속위성인 천리안위성 2A호 웹 서비스 서브시스템 및 환경위성 2B호 통합 자료처리 서브시스템에 대한 웹 개발을 수행하였습니다.
그리고 해솔 블로그에서는 다양한 기상학/천문학 정보와 더불어 사무 자동화/프로그래밍 언어를 소개하오니 방문 부탁드립니다.
좋은 하루 보내세요.

[재능플랫폼] 오투잡

[IT개발 - 응용프로그래밍] 통계 분석, 데이터 분석, 시각화를 성실하게 해 드립니다. - 재능마켓 �

판매가격:10,000원, [소개] - 데이터산업진흥원 데이터 가공 공급기업 선정 - 정보통신산업 진흥원 데이터 가공 공급기업 선정 - 다년간 축적된 경험 노하우를 바탕으로 개개인에게 맞춤형 솔루션�

www.otwojob.com

[재능플랫폼] 크몽

데이터수집, 파싱, 크롤링 해 드립니다. | 50,000원부터 시작 가능한 총 평점 0점의 IT·프로그래밍,

0개 총 작업 개수 완료한 총 평점 0점인 shlee1990의 IT·프로그래밍, 데이터분석·리포트, 데이터 마이닝·크롤링 서비스를 0개의 리뷰와 함께 확인해 보세요. IT·프로그래밍, 데이터분석·리포트, 데

kmong.com

요청

[세부 사항]

과제 1 : 모집단 크기 n, 모집단 평균, 모집단 분산, 모집단 범위, 최소 수, 최대 수, 모집단 모드 및 모집단 중앙값을 찾습니다.
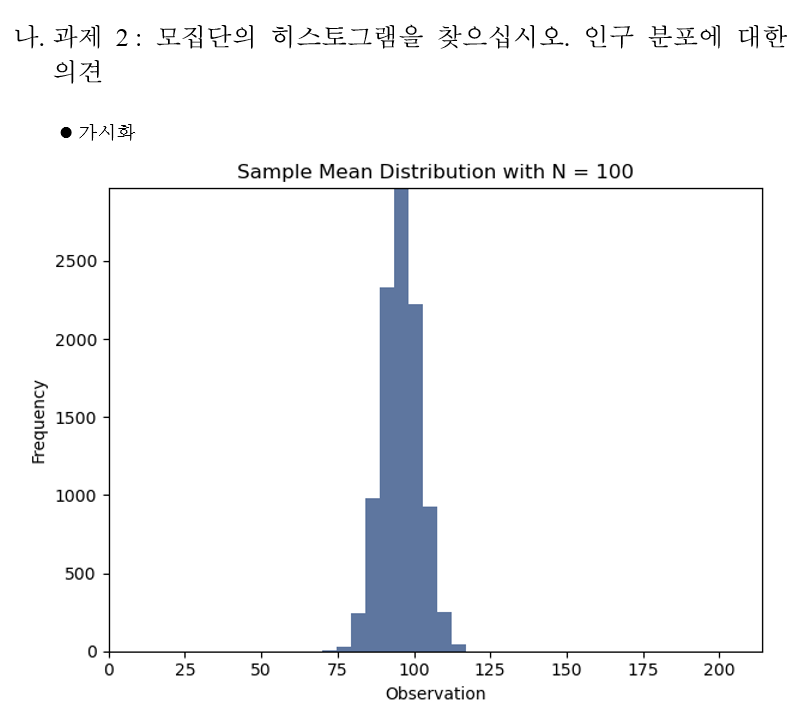
과제 2 : 모집단의 히스토그램을 찾으십시오. 인구 분포에 대한 의견
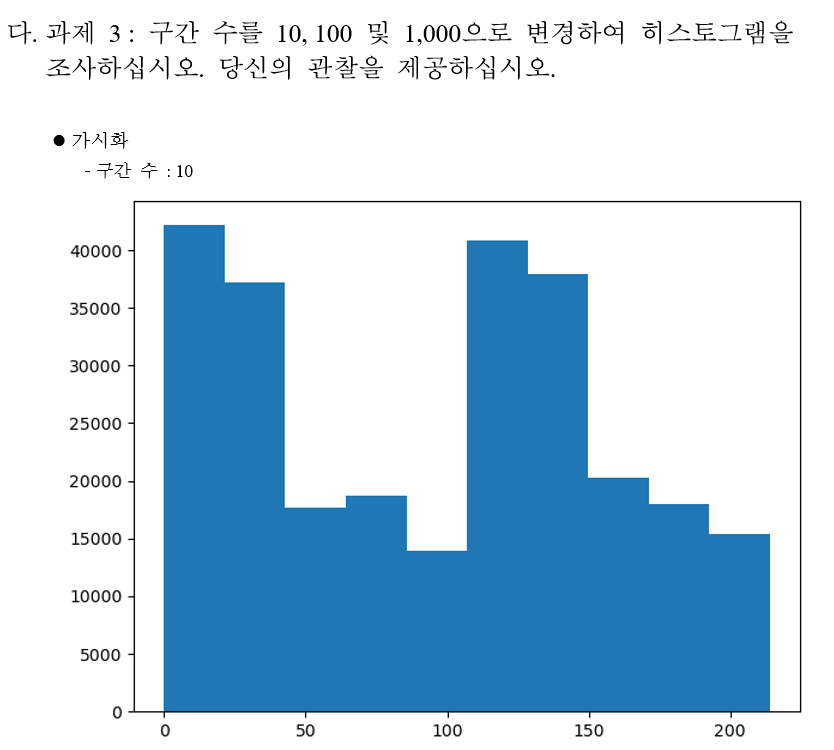
과제 3 : 구간 수를 10, 100 및 1,000으로 변경하여 히스토그램을 조사하십시오. 당신의 관찰을 제공하십시오.
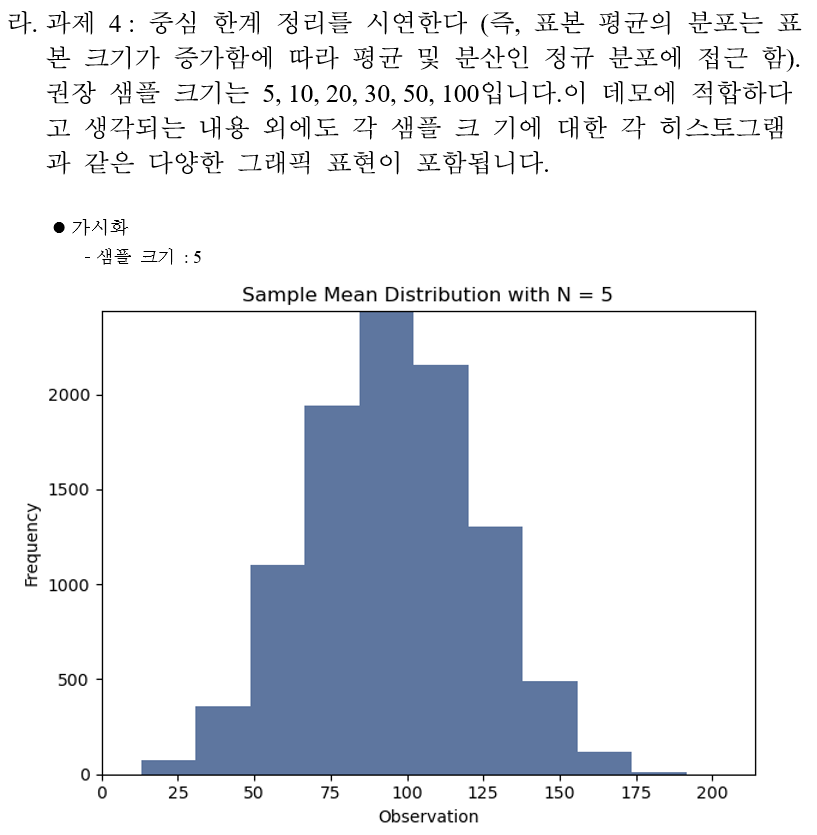
과제 4 : 중심 한계 정리를 시연한다 (즉, 표본 평균의 분포는 표본 크기가 증가함에 따라 평균 및 분산인 정규 분포에 접근 함). 권장 샘플 크기는 5, 10, 20, 30, 50, 100입니다.이 데모에 적합하다고 생각되는 내용 외에도 각 샘플 크 기에 대한 각 히스토그램과 같은 다양한 그래픽 표현이 포함됩니다.

완료

[사용 OS]

Windows 10

[사용 언어]

Python v3.8.5

[명세]

라이브러리 읽기 및 로그 설정

from PIL import Image
import sys
import numpy as np
import logging as log
import matplotlib.pyplot as plt
from src.util import central_limit_theorem as clt

# 로그 설정
log.basicConfig(stream=sys.stdout, level=log.INFO, format="%(asctime)s [%(threadName)-12.12s] [%(levelname)-5.5s] %(message)s")

이미지 파일 읽기

# 이미지 읽기
image = Image.open("D:/02. 블로그/PyCharm/resources/image/lena_gray.gif")

arrVal2D = np.array(image)
arrVal1D = arrVal2D.flatten()

기술 통계량 계산

# 이미지 읽기
image = Image.open("D:/02. 블로그/PyCharm/resources/image/lena_gray.gif")

arrVal2D = np.array(image)
arrVal1D = arrVal2D.flatten()

log.info("=================== 과제 1 ===================")
log.info("모집단 크기 : {%s}", arrVal1D.size)
log.info("모집단 평균 : {%s}", round(np.mean(arrVal1D), 2))
log.info("모집단 분산 : {%s}", round(np.var(arrVal1D), 2))
log.info("모집단 최대값 : {%s}", np.max(arrVal1D))
log.info("모집단 최소값 : {%s}", np.min(arrVal1D))
log.info("모집단 중앙값 : {%s}", np.median(arrVal1D))

모집단의 히스토그램 시각화

log.info("=================== 과제 2 ===================")
plt.hist(arrVal1D)
plt.show()

구간 수(10, 100, 1000)에 따른 히스토그램 시각화

log.info("=================== 과제 3 ===================")
binList = [10, 100, 1000]

for i in binList:
    plt.hist(arrVal1D, bins=i)
    plt.show()

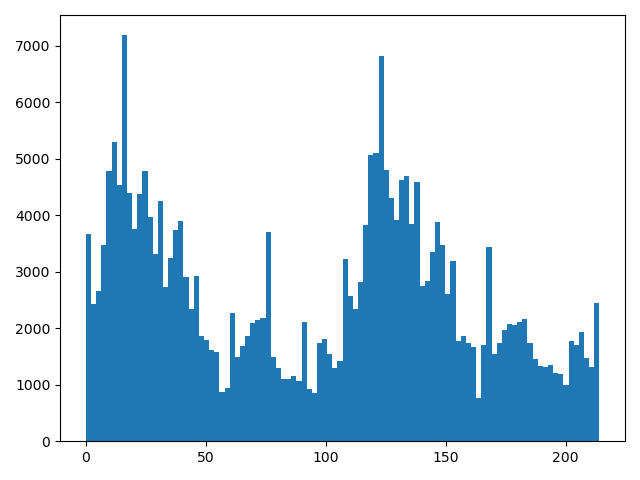
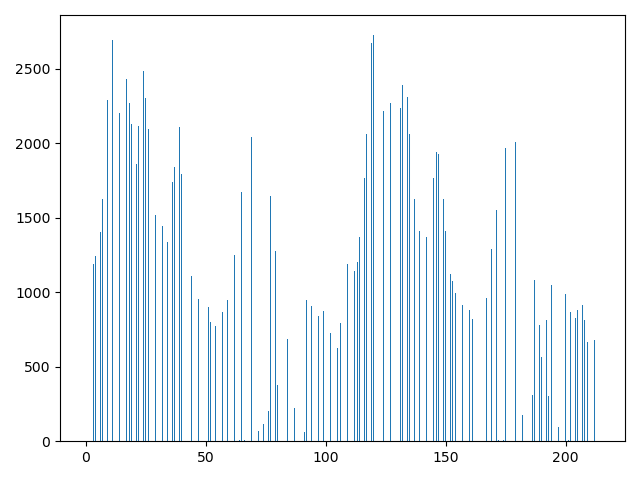
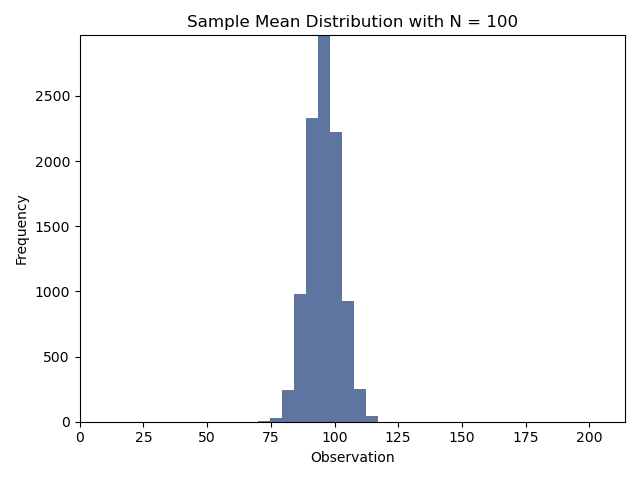
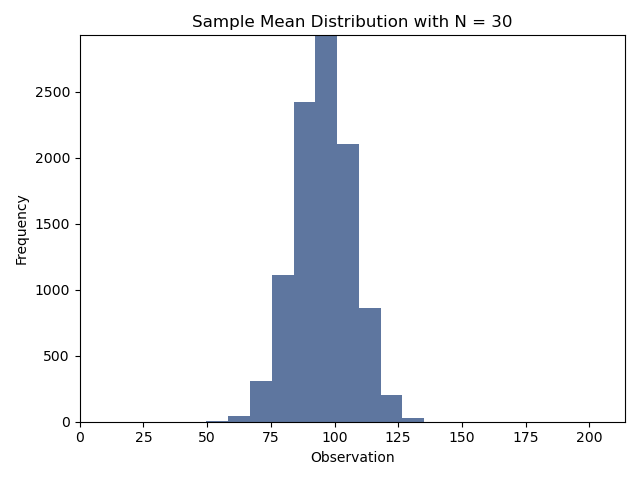
중심 극한 정리에 대한 시연

log.info("=================== 과제 4 ===================")
callClt = clt.CentralLimitTheorem(arrVal1D)
sampleList = [5, 10, 20, 30, 50, 100]
for sample in sampleList:
    callClt.run_sample(N=sample, plot=True, num_bins=None)

중심 극한을 위한 사용자 함수

import random
import numpy as np
import logging as log
import sys

log.basicConfig(stream=sys.stdout, level=log.INFO, format="%(asctime)s [%(threadName)-12.12s] [%(levelname)-5.5s] %(message)s")

class CentralLimitTheorem(object):

    def __init__(self, distribution):
        self.distribution = distribution
        self.dist_min = np.min(distribution)
        self.dist_max = np.max(distribution)
        self.dist_mean = np.mean(distribution)

    def _sample(self, N):
        sampleSum = 0
        for i in range(N):
            sampleSum += random.choice(self.distribution)
        return float(sampleSum) / float(N)

    def run_sample(self, N, plot = False, num_bins = None):
        means = []
        for i in range(10000):
            means.append(self._sample(N))
        if plot:
            title = "Sample Mean Distribution with N = %s" % N
            plot_distribution(means, title , self.dist_min, self.dist_max, num_bins)

            log.info("[샘플 크기: %s개] 모집단 평균 - 표본 평균 : {%s}", N, round(self.dist_mean - np.mean(means), 2))
        return means

def plot_distribution(distribution, title = None, bin_min = None, bin_max = None, num_bins = None):
    import matplotlib.pyplot as plt
    import seaborn as sns
    sns.set_palette("deep", desat=.65)
    if num_bins != None:
        bin_size = (bin_max - bin_min) / num_bins
        manual_bins = range(bin_min, bin_max + bin_size, bin_size)
        [n, bins, patches] = plt.hist(distribution, bins = manual_bins)
    else:
        [n, bins, patches] = plt.hist(distribution)
    if title != None:
        plt.title(title)
    plt.xlim(bin_min, bin_max)
    plt.ylim(0, max(n) + 2)
    plt.ylabel("Frequency")
    plt.xlabel("Observation")
    plt.show()

[소스 코드]

from PIL import Image
import sys
import numpy as np
import logging as log
import matplotlib.pyplot as plt
from src.util import central_limit_theorem as clt

# 로그 설정
log.basicConfig(stream=sys.stdout, level=log.INFO, format="%(asctime)s [%(threadName)-12.12s] [%(levelname)-5.5s] %(message)s")

# 이미지 읽기
image = Image.open("D:/02. 블로그/PyCharm/resources/image/lena_gray.gif")

arrVal2D = np.array(image)
arrVal1D = arrVal2D.flatten()

log.info("=================== 과제 1 ===================")
log.info("모집단 크기 : {%s}", arrVal1D.size)
log.info("모집단 평균 : {%s}", round(np.mean(arrVal1D), 2))
log.info("모집단 분산 : {%s}", round(np.var(arrVal1D), 2))
log.info("모집단 최대값 : {%s}", np.max(arrVal1D))
log.info("모집단 최소값 : {%s}", np.min(arrVal1D))
log.info("모집단 중앙값 : {%s}", np.median(arrVal1D))

log.info("=================== 과제 2 ===================")
plt.hist(arrVal1D)
plt.show()

log.info("=================== 과제 3 ===================")
binList = [10, 100, 1000]

for i in binList:
    plt.hist(arrVal1D, bins=i)
    plt.show()

log.info("=================== 과제 4 ===================")
callClt = clt.CentralLimitTheorem(arrVal1D)
sampleList = [5, 10, 20, 30, 50, 100]
for sample in sampleList:
    callClt.run_sample(N=sample, plot=True, num_bins=None)

[결과물]

결과 보고서

참고 문헌

[논문]

없음

[보고서]

없음

[URL]

없음

문의사항

[기상학/프로그래밍 언어]

sangho.lee.1990@gmail.com

[해양학/천문학/빅데이터]

saimang0804@gmail.com

저작자표시 비영리 변경금지

'자기계발 > 재능상품' 카테고리의 다른 글

[재능상품] R을 이용한 diamonds 자료 전처리 (0)	2020.11.10
[재능상품] R을 이용한 학술연구정보서비스 크롤링 및 클라우드 시각화 (0)	2020.11.10
[재능상품] R을 이용한 부트스트랩 방법을 이용한 표본 평균 및 히스토그램 가시화 (0)	2020.10.18
[재능상품] R을 이용한 프로그래밍 과제 (0)	2020.10.18
[재능상품] Shell Script를 이용한 Bingo 함수 버전, 재귀 처리, 숫자 야구 (0)	2020.10.18

정보

내용