정보
-
업무명 : R을 이용한 통계 분석 및 데이터 시각화 : 그림으로 수식 표기
-
작성자 : 박진만
-
작성일 : 2020-04-03
-
설 명 :
-
수정이력 :
내용
[개요]
-
R은 통계 분석 및 시각화 등의 기능을 갖춘 프로그래밍 언어 내지 통계 분석 환경입니다.
-
통계 분석 기능으로 통계 검정, 선형 회귀 분석, 시계열 데이터 분석, 클러스터링 등을 지원하고 있습니다.
-
또한 최신 논문에서 발표된 같은 새로운 기술도 R로 구현되는 경우가 많습니다.
-
특히 시각화 기능으로 히스토그램, 막대 그래프, 선 그래프, 산포도, 나무 모양 그림이나 히트맵 등 기본적인 그래프가 기본으로 지원하고 있습니다.
-
또한 ggplot2 등의 패키지를 사용하여 더 높은 수준의 그림을 가시화할 수 있습니다.

[특징]
-
데이터를 이해하기 위해서 통계 분석 및 데이터 시각화가 요구되며 이 프로그램은 이러한 목적을 달성하기 위한 소프트웨어
[기능]
-
데이터형 소개
[활용 자료]
-
없음
[자료 처리 방안 및 활용 분석 기법]
-
없음
[사용법]
-
소스 코드 예시 참조
[사용 OS]
-
Windows 10
[사용 언어]
-
R v3.6.2
-
R Studio v1.2.5033
소스 코드
[수식 표기]
-
expression함수를 이용하면 적분과 극한 같은 복잡한 수식을 작성할 수있다.
-
이것을 이용하면 그래프 이미지에 수식을 겹쳐서 쓰는 것이 가능하게 된다.
[기본 수식]
-
아래의 예시는 사칙 연산이나 등호 등을 나타내는 수식 기호를 표기하는 방법의 예시이다.
plot(0, 0, type = "n", xlim = c(0, 3), ylim = c(0, 9), xlab = "", ylab = "")
text(1, 8, expression(a + b), cex = 1.3)
text(1, 7, expression(a - b), cex = 1.3)
text(1, 6, expression(a * b), cex = 1.3)
text(1, 5, expression(a / b), cex = 1.3)
text(1, 4, expression(a %+-% b), cex = 1.3)
text(1, 3, expression(a %*% b), cex = 1.3)
text(1, 2, expression(a %.% b), cex = 1.3)
text(1, 1, expression(a %/% b), cex = 1.3)
text(2, 8, expression(a == b), cex = 1.3)
text(2, 7, expression(a != b), cex = 1.3)
text(2, 6, expression(a < b), cex = 1.3)
text(2, 5, expression(a >= b), cex = 1.3)
text(2, 4, expression(a %~~% b), cex = 1.3)
text(2, 3, expression(a %=~% b), cex = 1.3)
text(2, 2, expression(a %==% b), cex = 1.3)
text(2, 1, expression(a %prop% b), cex = 1.3)
[수식]
-
아래는 근호와 및 각종 기호 등을 R의 expression함수로 그리는 예시이다.
plot(0, 0, type = "n", xlim = c(0, 4), ylim = c(0, 9), xlab = "", ylab = "")
text(1, 8, expression(x[i]), cex = 1.3)
text(1, 7, expression(x^2), cex = 1.3)
text(1, 6, expression(paste(x, y, z)), cex = 1.3)
text(1, 5, expression(sqrt(x)), cex = 1.3)
text(1, 4, expression(sqrt(x, 2)), cex = 1.3)
text(1, 3, expression(hat(x)), cex = 1.3)
text(1, 2, expression(tilde(x)), cex = 1.3)
text(1, 1, expression(dot(x)), cex = 1.3)
text(2, 8, expression(ring(x)), cex = 1.3)
text(2, 7, expression(plain(x)), cex = 1.3)
text(2, 6, expression(bold(x)), cex = 1.3)
text(2, 5, expression(italic(x)), cex = 1.3)
text(2, 4, expression(bolditalic(x)), cex = 1.3)
text(2, 3, expression(symbol(x)), cex = 1.3)
text(2, 2, expression(list(x, y, z)), cex = 1.3)
text(2, 1, expression(cdots), cex = 1.3)
text(3, 8, expression(x %subset% y), cex = 1.3)
text(3, 7, expression(x %subseteq% y), cex = 1.3)
text(3, 6, expression(x %notsubset% y), cex = 1.3)
text(3, 5, expression(x %supset% y), cex = 1.3)
text(3, 4, expression(x %<->% y), cex = 1.3)
text(3, 3, expression(x %=>% y), cex = 1.3)
text(3, 2, expression(x %dblup% y), cex = 1.3)
text(3, 1, expression(x %dbldown% y), cex = 1.3)
[기타 복잡한 수식]
-
아래는 적분 기호 등을 R의 expression함수로 그리는 예시이다.
plot(0, 0, type = "n", xlim = c(0,4), ylim = c(0, 9), xlab = "", ylab = "")
# 적분
text(1, 8, expression(paste(
integral(f(x), 0, infinity),
dx == 1
)), cex = 1.5)
# 분수의 극한
text(1, 6, expression(
lim(over(sin(x), x), x %->% 0) == 1
), cex = 1.5)
# 시그마 기호
text(1, 4, expression(
sum(j, j == 1, n) == over(n(n+1), 2)
), cex = 1.5)
# 곱 기호
text(1, 2, expression(
prod(plain(P)(X == x), x)
), cex = 1.5)
# 기타 복잡한 수식의 예시
text(3, 8, expression(
lim(
sum(
((over(k, n))^2 %.% over(1, n)),
k == 1,
n
),
n %->% infinity
)
==
integral(x^2, 0, 1) * dx
), cex = 1.5)
# 기타 복잡한 수식의 예시 2
text(3, 6, expression(
hat(f(xi)) %==%
integral(
g(xi),
- infinity,
infinity
)
*
e^(2 * pi * i * x * xi)
*
d * xi
), cex = 1.5)
# 기타 복잡한 수식의 예시 3
text(3, 4, expression(
f(x) ==
sum(
over(f^(n) * (a), n)
,n == 0
,infinity
)
*
(x - a)^n + R[n]
), cex = 1.5)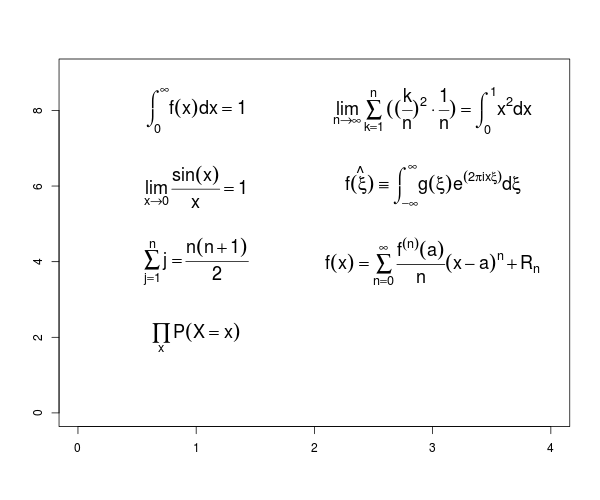
[다음글]
[R] R을 이용한 통계 분석 및 데이터 시각화 : 그래프 범례
정보 업무명 : R을 이용한 통계 분석 및 데이터 시각화 : 그래프 범례 작성자 : 박진만 작성일 : 2020-04-03 설 명 : 수정이력 : 내용 [개요] R은 통계 분석 및 시각화 등의 기능을 갖춘 프로그래밍 언어 내지 통..
shlee1990.tistory.com
[이전글]
[R] R을 이용한 통계 분석 및 데이터 시각화 : 히트맵
정보 업무명 : R을 이용한 통계 분석 및 데이터 시각화 : 히트맵 작성자 : 박진만 작성일 : 2020-04-03 설 명 : 수정이력 : 내용 [개요] R은 통계 분석 및 시각화 등의 기능을 갖춘 프로그래밍 언어 내지 통계 분..
shlee1990.tistory.com
참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com
본 블로그는 파트너스 활동을 통해 일정액의 수수료를 제공받을 수 있음
'프로그래밍 언어 > R' 카테고리의 다른 글
| [R] R을 이용한 통계 분석 및 데이터 시각화 : 이중축 (0) | 2020.04.03 |
|---|---|
| [R] R을 이용한 통계 분석 및 데이터 시각화 : 그래프 범례 (0) | 2020.04.03 |
| [R] R을 이용한 통계 분석 및 데이터 시각화 : 히트맵 (0) | 2020.04.03 |
| [R] R을 이용한 통계 분석 및 데이터 시각화 : 입체 산포도 (0) | 2020.04.03 |
| [R] R을 이용한 통계 분석 및 데이터 시각화 : 산포도 (0) | 2020.04.03 |

