정보
-
업무명 : 2016년 2학기 전선 자료분석과 가시화 과제물
-
작성자 : 이상호
-
작성일 : 2020-03-18
-
설 명 :
-
수정이력 :
내용
[개요]
-
안녕하세요? 기상 연구 및 웹 개발을 담당하고 있는 해솔입니다.
-
오늘은 대학원 석사 3학기에 배운 자료분석과 가시화에 대한 내용을 다루고자 합니다.
-
특히 배운 지식를 활용하여 각 주차별 발표 및 토의는 학술 논문 또는 보고서를 작성 시 많은 도움이 되었습니다.
-
그에 따른 자료분석과 가시화의 "과제물"을 소개해 드리고자 합니다.
[특징]
-
자료분석과 가시화 수업에 대한 이해를 돕기위해 작성
[기능]
-
과제물
-
소스 코드
-
관련 자료
[사용 OS]
-
Windows 10
[사용 언어]
-
Fortran 90
과제물
[미 산란 (Mie Scattering)]
QSCAT 소스 코드를 이용하여 다음 조건 하에서 결과 Report를 작성하여 제출하시오.
[조건] 엑셀 첨부 파일에서 파장별 굴절률 자료 참조하여 4가지 입자 (Dust-like, Water soluble, Oceanic, Soot)별 굴절률 (실수부, 허수부) 자료 이용
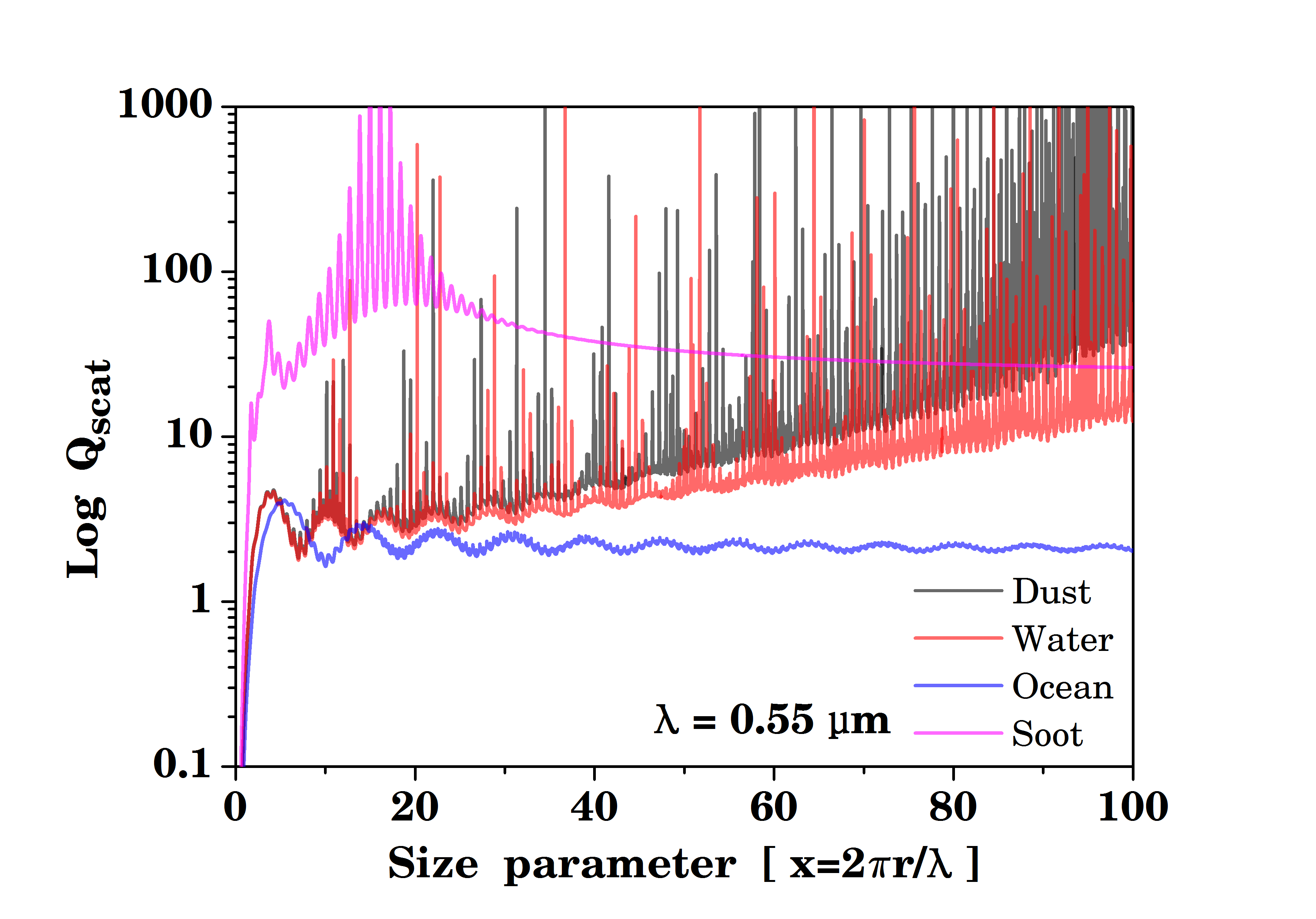
[과제 1] 4가지 입자별, 산란효율 (QSCAT) vs 입자 크기에 관한 그래프 작성 및 비교 설명
[과제 2] Dust-like 입자에 대하여 입자 크기 = 0.1, 1, 5, 10 um, 550 nm인 경우에서의 산란위상함수 (phase function)를 polar plot 작성 및 비교 설명
[과제 3] 4가지 입자에 대하여 각각 파장별, 입자크기별, 산란계수 (Cext) 3D 또는 2D contour 그래프 작성 및 비교 설명

[과제 1] 4가지 입자별, 산란효율 (QSCAT) vs 입자 크기에 관한 그래프 작성 및 비교 설명
-
입자의 산란이론에 의하여 각 입자의 굴절률과 크기분포는 광 산란 및 흡수 효과를 계산할 때 필요하며, 이를 WCP112 Table을 인용하여 사용하였다. 입자의 굴절률은 각 파장에 따라 실수부와 허수부로 나뉘며 이를 입력자료로 하는 미 산란 코드(QSCAT.f)를 통해 이론적으로 계산하였다.
-
이때 입자의 모양은 구형으로 가정하였고, 입자 크기는 로 계산하였다. 이러한 구형과 비구형 입자의 광학 특성값은 5-8 % 차이로 보고된 바 있다.
-
그림 1은 파장 0.55 µm에서 입자크기와 산란 효율을 입자별로 나타냈으며, x축은 입자 크기와 y축은 Log 스케일의 산란 효율이다. Dust와 Water의 경우 입자 크기가 0~10에서 산란효율이 비슷한 수준을 보였으나 그 이후로 Dust가 Water에 비해 최대 산란효율을 나타내었다. 또한 입자 크기가 증가할수록 산란 효율이 증가하였다.
-
이와 달리 Soot의 경우, 입자 크기가 20에서 최대 산란효율 나타내며, 입자가 증가할수록 산란효율이 일정하게 나타내었다. 또한 Ocean도 유사한 경향을 띠며 최대 산란효율은 5에서 나타내었다.
-
이와 같이 WCP112 Table에서 언급된 0.55 µm의 굴절률은 해당 입자간 산란 특성에 차이를 발생시켰으며, 입자 크기가 증가할수록 뚜렷한 차이를 나타내었다. 또한, 0.55 µm을 기준으로 입자크기가 작을 때 레일라이 산란이 발생되며, 입자크기가 클 때 미 산란이 발생되는 특성이 있다.
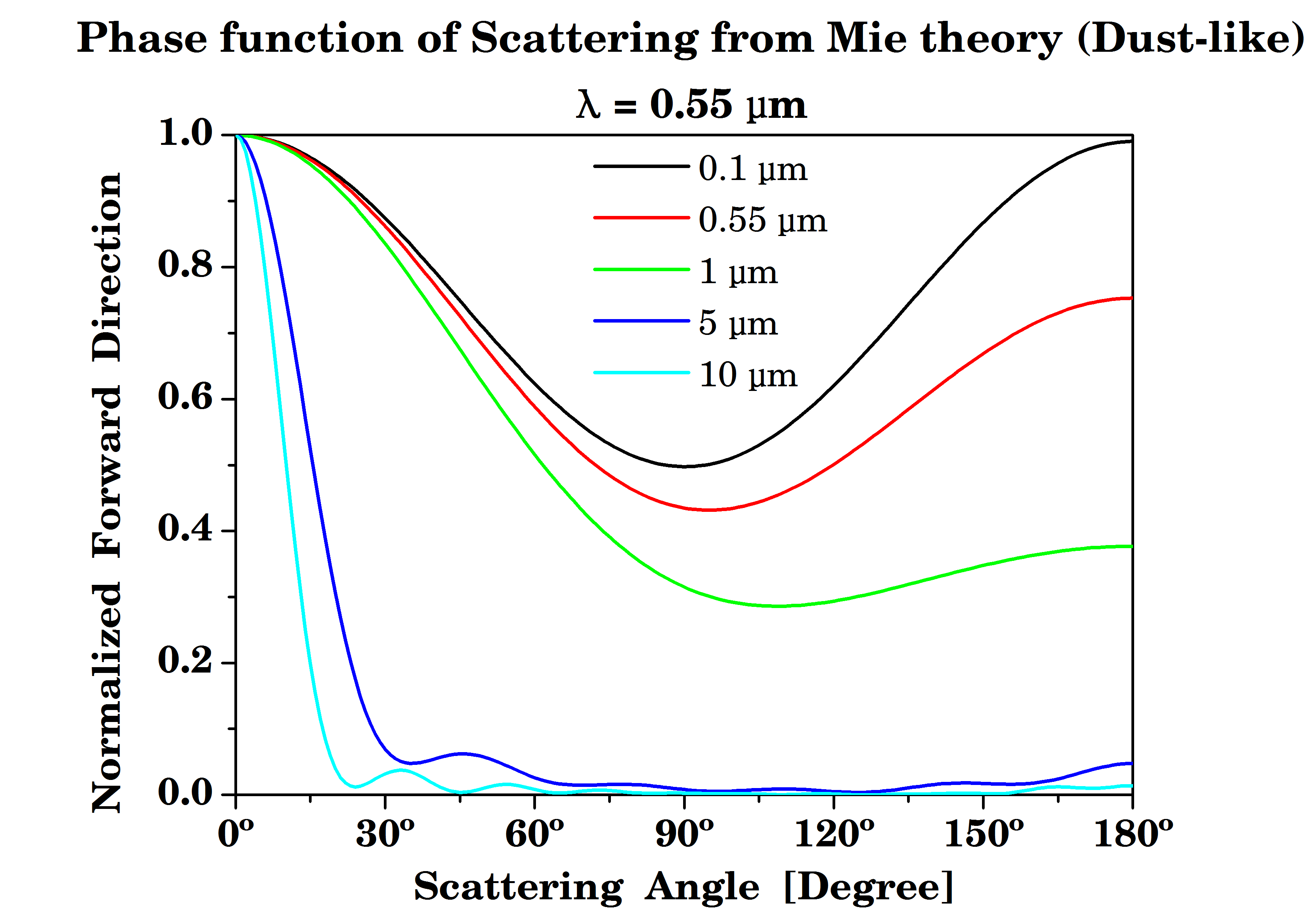
[과제 2] Dust-like 입자에 대하여 입자 크기 = 0.1, 1, 5, 10 um, 550 nm인 경우에서의 산란위상함수 (phase function)를 polar plot 작성 및 비교 설명
-
그림 2a은 파장 0.55 um, Dust-like 입자에 대하여 산란 각도에 따른 Normalized Forward Direction(이하 NFD)로 나타내며 x축은 산란 각도와 y축은 NTD이다.
-
또한 산란각이 0~60˚(전방산란; 빨강 음영), 60~120˚(측방산란; 파란 음영), 120~180˚(후방산란; 초록 음영)으로 나타내었다.
-
입자 크기가 0.1 um인 경우, NTD는 산란각이 0˚인 경우에 최대이고 산란각이 증가할수록 NTD가 감소하여 60~120˚ 근처에서 최소값이 나타내고 120~180˚ 사이에서 NTD가 오히려 증가하고 있다.
-
이때 빛의 파장에 비해 입자 크기가 작기 때문에 레일라이 산란이 발생되며, 전방산란이 된 양만큼 후방 산란되어 나타난다 (그림 2b, 그림 2c 참조).
-
이와 달리 빛의 파장에 비해 입자 크기가 비슷하거나 큰 경우, 미 산란이 발생되며 전방산란이 현저하고 상대적으로 작은 에너지가 측방, 후방으로 산란된다 (그림 2b, 그림 2c 참조).
-
이때 레일라이 산란과 달리 파장이 길거나 짧거나 파장에 의하여 산란의 강도가 변하지 않고 입자 크기, 종류, 모양에 등에 변화한다.
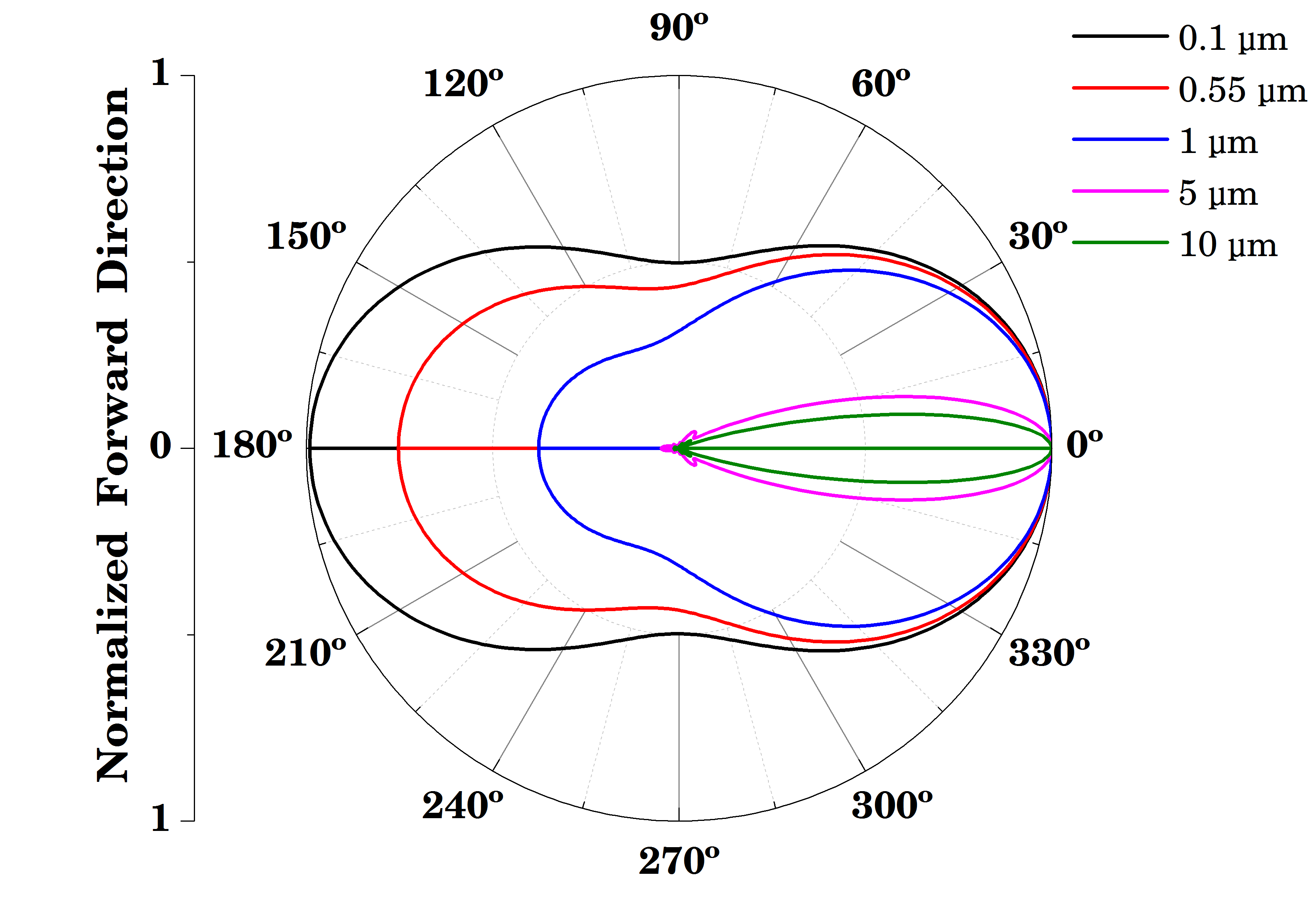
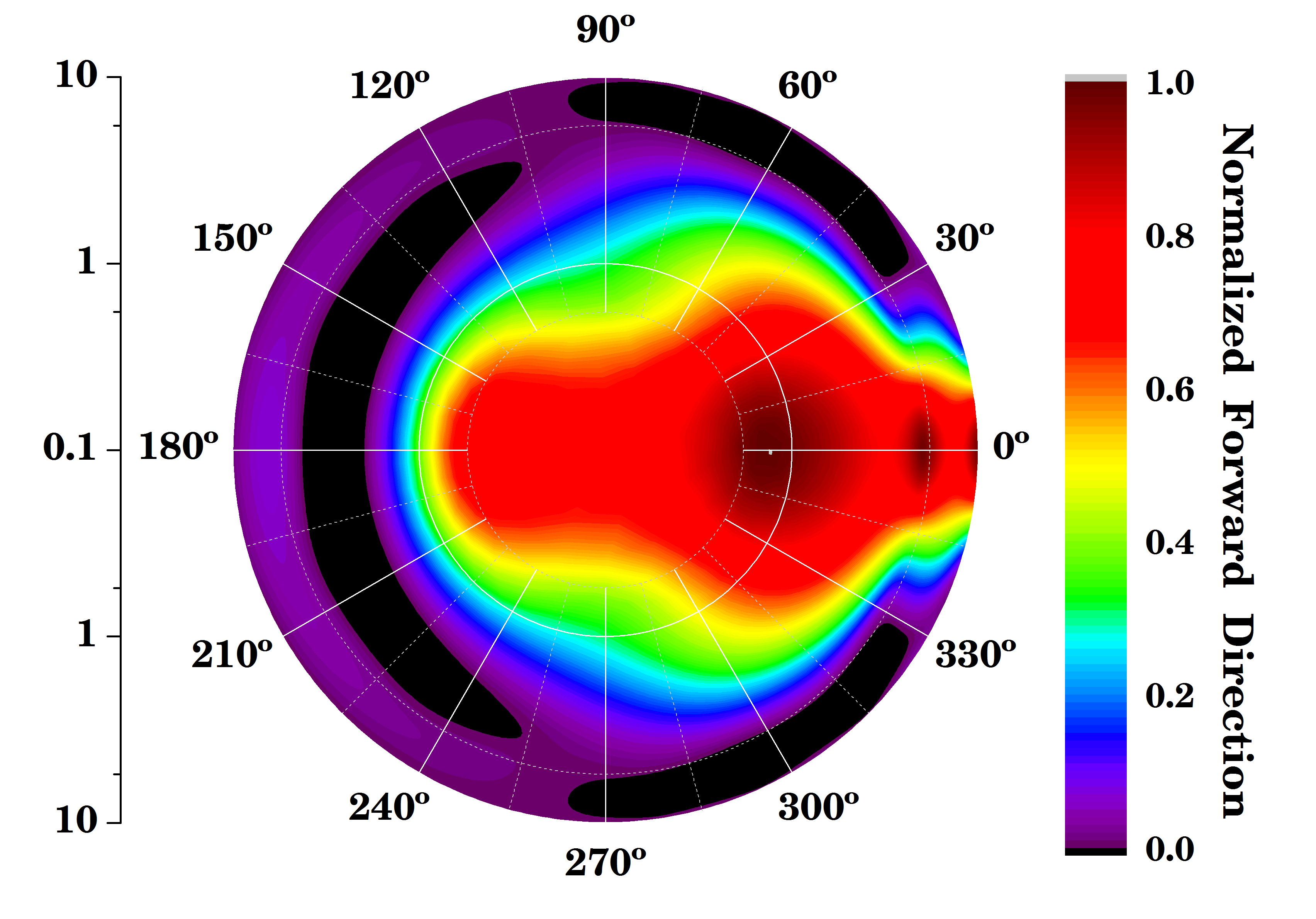
[과제 3] 4가지 입자에 대하여 각각 파장별, 입자크기별, 산란계수 (Cext) 3D 또는 2D contour 그래프 작성 및 비교 설명
-
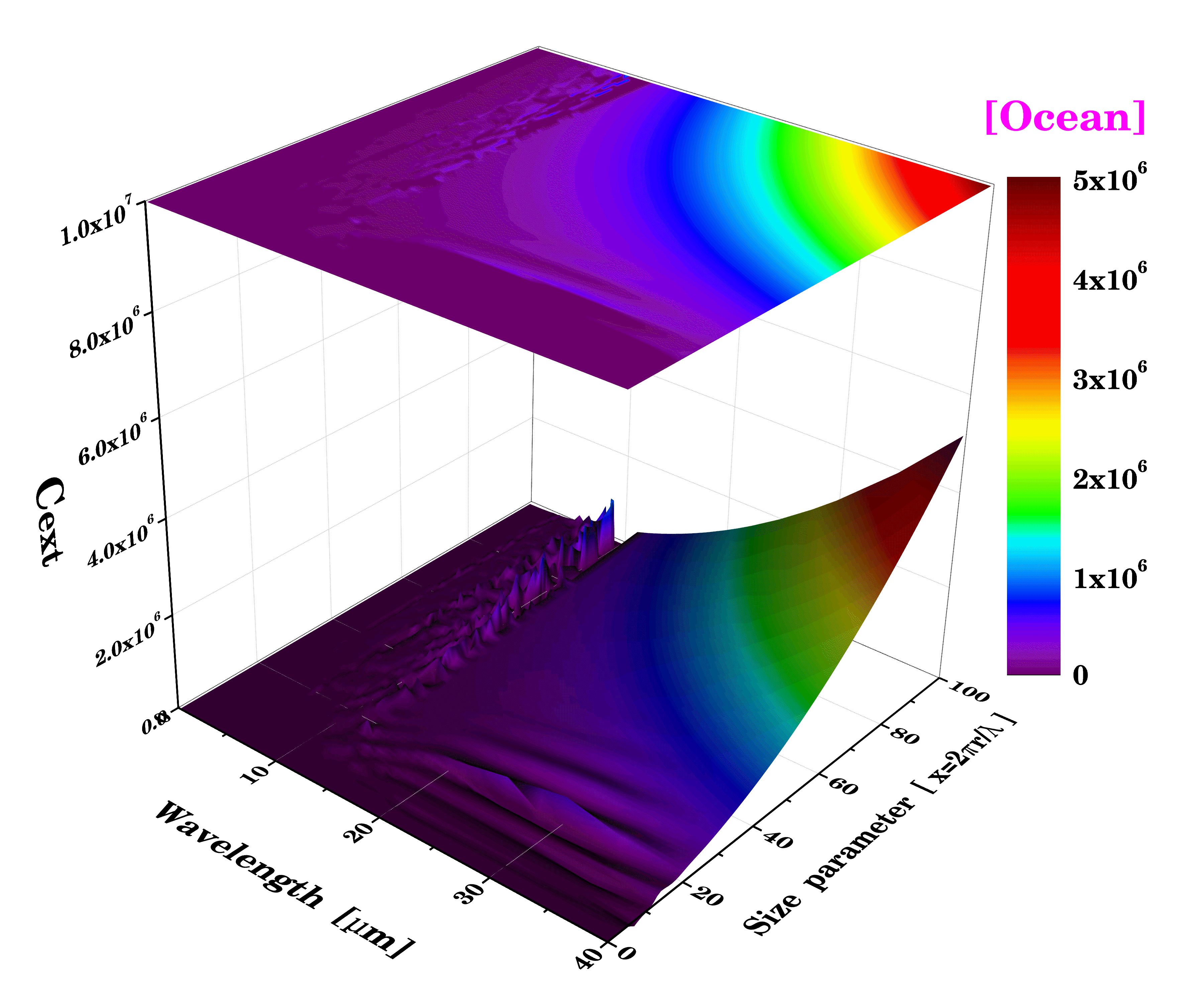
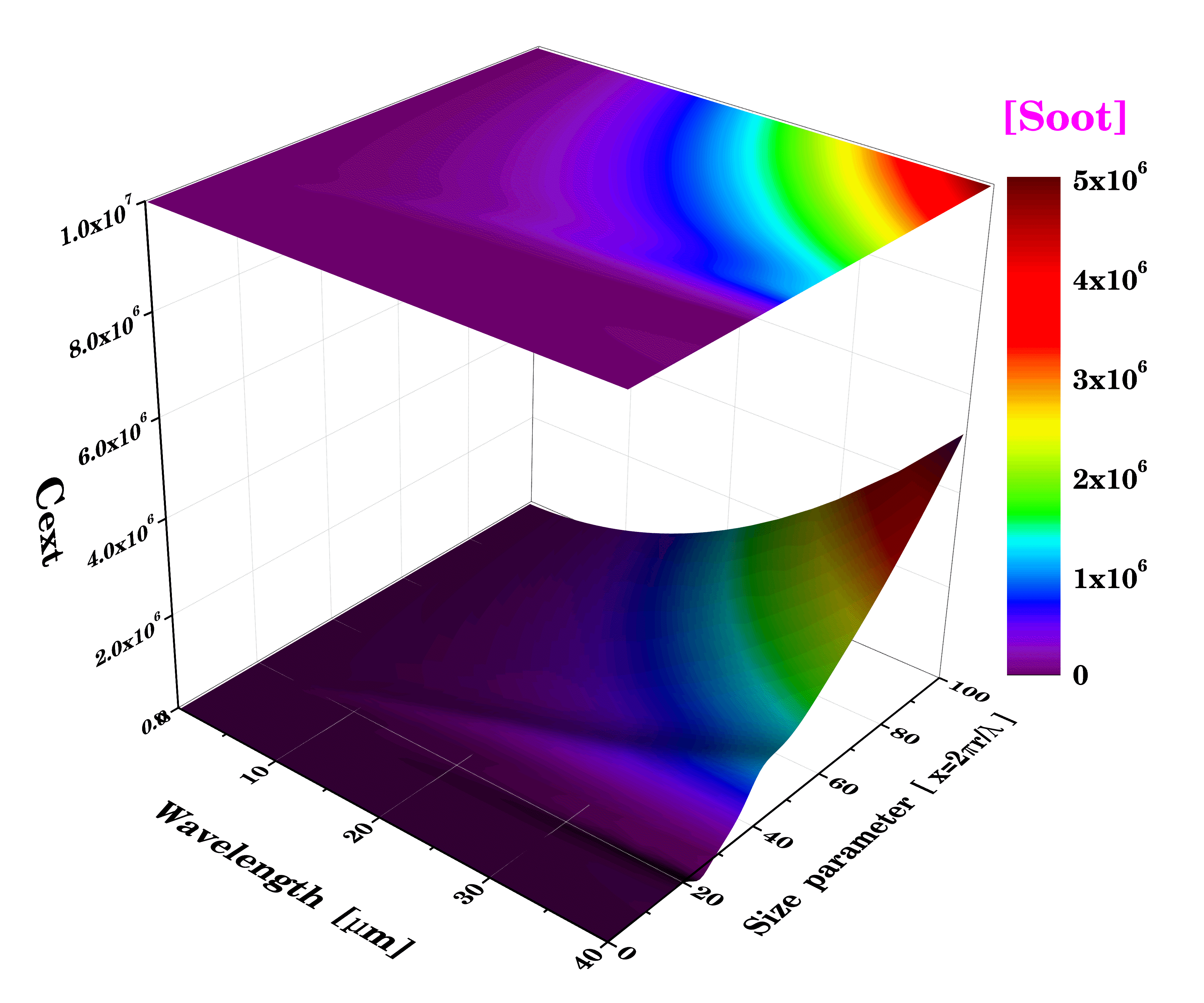
그림 3은 입자들에 대하여 각 파장, 입자크기에 따른 산란계수를 2D와 3D로 나타내었으며, x축은 파장 (0-40 µm)과 y축은 입자 크기 (0-100) 그리고 z축은 산란 계수이다.
-
Dust인 경우, 그림 3a와 같이 입자 크기 (0-20)에서 각 파장별 산란계수와 파장 (0-8 µm)에서 각 입자별 산란계수는 일정하게 나타나며 파장이 8 µm 이후에 각 파장별 입자별 산란계수가 증가함을 나타났다.
-
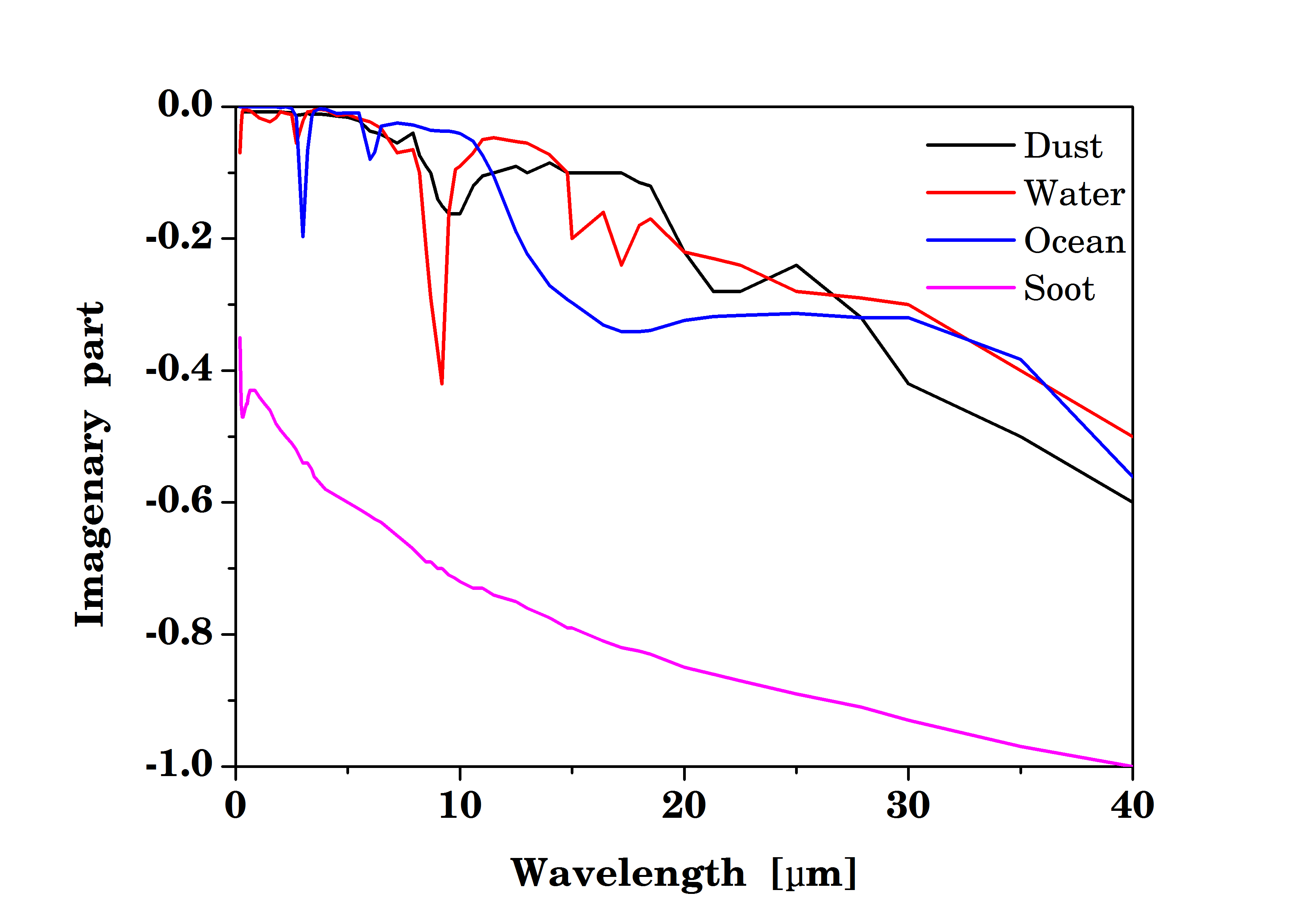
이와 같이 8 µm에서 산란계수는 변화가 나타나는 이유는 그림 4a와 같이 Dust에서 굴절률의 실수부가 증가 때문이다. 또한 파장이 30 µm 이상 영역과 입자 크기가 20 이상 영역에서 산란계수가 선형적으로 증가를 보였다.
-
Water인 경우, 그림 3b와 같이 Dust와 유사한 경향을 띠며 특히, 8 µm에서 다른 입자에 비하여 최대 산란계수를 나타났으며 이는 앞서 설명된 바와 일치한다.
-
Ocean인 경우, 그림 3c와 같이 Dust, Water와 유사한 경향을 띠며 8 µm에서 다른 입자에 비하여 최소 산란계수를 나타났으며, 이는 굴절률의 실수부가 감소하기 때문으로 기인된다.
-
이와 달리 Soot은 그림 4a와 같이 굴절률의 실수부가 다른 입자에 비해 큰 폭으로 증가함에도 불구하고 그림 4d에서 입자 크기와 파장별에 따른 산란계수는 뚜렷한 변화없이 선형적으로 증가함을 보였다. 이는 그림 4a, b와 같이 굴절률의 실수부는 증가하고 굴절률의 허수부가 감소하여 두 요소의 상쇄되었기 때문이다.



소스 코드
[미 산란 (Mie Scattering]
-
미 산란 계산을 위한 포트란 (Fortran) 소스 코드
program qscat
c *****************************************************************
c you must make input file "input.dat"
c whic included
c ' nm(i4),1x,ri(f6.4),1x,si(f5.3)
c wavel(f6.3),refre(f7.3),3x,Refim(f12.10)'
c ****************************************************************
real, dimension(80, 10) :: dust, water, ocean, soot
complex refrel,s1(1000),s2(1000)
c *********************************************************
! open(unit=1,file='input.dat')
open(11, file='WCP112.table', status='old')
open(unit=5,FILE='miesca.out',status='unknown')
open(unit=10,FILE='phase.out',status='unknown')
c *********************************************************
c refmed = (real) refractive index of surrounding medium
c =1 (air)
c **********************************************************
refmed=1.0
c **********************************************************
c read particle size distribution parameter
c **********************************************************
! read(1,1)ri
!1 format(f6.3)
! write(5,*)ri
c2 format(5x,'nm=',f6.3)
c *********************************************************
c refractive index of sphere = refre + i*refim
c *********************************************************
! read(1,*)wavel,refre,refim
!4 format(f6.3,f6.3,f6.3)
! LSH
do ii = 1, 61
read(11,*) wavel, dust(ii,1:2), water(ii,1:2),
& ocean(ii,1:2), soot(ii,1:2)
refre = dust(ii,1)
refim = dust(ii,2)
! refre = water(ii,1)
! refim = water(ii,2)
! refre = ocean(ii,1)
! refim = ocean(ii,2)
! refre = soot(ii,1)
! refim = soot(ii,2)
write(*,*) wavel, refre, refim
refrel=cmplx(refre,refim)/refmed
c write (5,*) wavel,refre,refim
c5 format(5x,'wavelength=',f6.3,2x,'refre=',f7.3,2x,'refim=',f12.10)
c write (5,11)
!11 format (//,7x,'x',8x,'dp',10x,'QSCAT',8x,'QEXT',10x,'QBACK',8x,
! +'CSCAT',9x,'CEXT',9x,'CBACK')
! LSH
! do ri=0.0, 100000.0, 0.1
do i=1, 1
ri = 0.55
c **********************************************************
c Diameter (nm) and wavelength (wavel) same units
c **********************************************************
x=3.14159265*2.0*ri*refmed/wavel
! write(*,*) x
! write(*,*) refrel
c ***********************************************************
c nang = number of angles between 0 and 90 degrees
c matrix elements calculates at 2*nang-1 angles
c including 0, 90, and 180 degrees
c ***********************************************************
nang=91
dang=1.570796327/float(nang-1)
call bhmie(x,refrel,nang,s1,s2,qext,qsca,qback)
csca=2.0*3.141592*(ri**2)*qsca
cext=2.0*3.141592*(ri**2)*qext
cback=2.0*3.141592*(ri**2)*qback
write(5,65) x,ri,qsca,qext,qback,csca,cext,cback
65 format (1x,f9.4,1x,f9.5,1x,e12.6,1x,e12.6,1x,e12.6,1x,e12.6,1x,
+e12.6,1x,e12.6)
c ************************************************************
c s33 and s34 matrix elements normalized by s11.
c s11 is normalized to 1.0 in the forward direction
c pol=degree of polarization (incident unpolarized light)
c *************************************************************
C
c GO TO 500
C
s11nor=0.5*(cabs(s2(1))**2+cabs(s1(1))**2)
nan=2*nang-1
do 355 j=1,nan
aj=j
s11=0.5*cabs(s2(j))*cabs(s2(j))
s11= s11+0.5*cabs(s1(j))*cabs(s1(j))
s12=0.5*cabs(s2(j))*cabs(s2(j))
s12= s12-0.5*cabs(s1(j))*cabs(s1(j))
pol=-s12/s11
s33=real(s2(j)*conjg(s1(j)))
s33= s33/s11
s34=aimag(s2(j)*conjg(s1(j)))
s34= s34/s11
s11= s11/ s11nor
ang=dang*(aj-1)*57.2958
355 write (10,75) ang,s11,pol,s33,s34
75 format (5x,f6.2,2x,e13.6,2x,e13.6,2x,e13.6,2x,e13.6)
C ************************************************
500 CONTINUE
C ***********************************************
700 continue
! LSH
write(99,'(7f15.4)') ri, qsca,qext,qback,csca,cext,cback
enddo ! i
enddo ! ii
stop
end
c *****************************************************************
c subroutine BHMIE calculates amplitude scattering matrix
c elements and efficiencies for extinction, total scattering
c and backscattering for a given size parameter and relative
c refractive index
c ******************************************************************
subroutine BHMIE (x,refrel,nang,s1,s2,qext,qsca,qback)
dimension amu(200),theta(200),pi(200),tau(200),pi0(200),pi1(200)
complex d(3000),y,refrel,xi,xi0,xi1,an,bn,s1(250),s2(250)
double precision psi0,psi1,psi,dn,dx
dx=x
y=x*refrel
c **********************************************
c series terminated after nstop terms
c **********************************************
xstop=x+4.*x**.3333+2.0
nstop=xstop
ymod=cabs(y)
nmx=amax1(xstop,ymod)+15
dang=1.570796327/float(nang-1)
do 555 j=1,nang
theta(j)=(float(j)-1.)*dang
555 amu(j)=cos(theta(j))
c ********************************************************
c logarithmic derivative d(j) calculated by downward
c recurrence beginning with initial value 0.0 + i*0.0
c at j = nmx
c ********************************************************
d(nmx)=cmplx(0.0,0.0)
nn=nmx-1
do 120 n=1,nn
rn=nmx-n+1
120 d(nmx-n)=(rn/y)-(1./(d(nmx-n+1)+rn/y))
do 666 j=1,nang
pi0(j)=0.0
666 pi1(j)=1.0
nn=2*nang-1
do 777 j=1,nn
s1(j)=cmplx(0.0,0.0)
777 s2(j)=cmplx(0.0,0.0)
c ****************************************************
c Riccati-Bessel functions with real argument x
c calculated by upward recurrence
c ****************************************************
psi0=dcos(dx)
psi1=dsin(dx)
chi0=-sin(x)
chi1=cos(x)
apsi0=psi0
apsi1=psi1
xi0=cmplx(apsi0,-chi0)
xi1=cmplx(apsi1,-chi1)
qsca=0.0
gsca=0.0
n=1
200 dn=n
rn=n
fn=(2.*rn+1.)/(rn*(rn+1.))
psi=(2.*dn-1.)*psi1/dx-psi0
apsi=psi
chi=(2.*rn-1.)*chi1/x-chi0
xi=cmplx(apsi,-chi)
an=(d(n)/refrel+rn/x)*apsi-apsi1
an=an/((d(n)/refrel+rn/x)*xi-xi1)
bn=(refrel*d(n)+rn/x)*apsi-apsi1
bn=bn/((refrel*d(n)+rn/x)*xi-xi1)
qsca=qsca+(2.*rn+1.)*(cabs(an)*cabs(an)+cabs(bn)*cabs(bn))
do 789 j=1,nang
jj=2*nang-j
pi(j)=pi1(j)
tau(j)=rn*amu(j)*pi(j)-(rn+1.)*pi0(j)
p=(-1.)**(n-1)
s1(j)=s1(j)+fn*(an*pi(j)+bn*tau(j))
t=(-1.)**n
s2(j)=s2(j)+fn*(an*tau(j)+bn*pi(j))
if(j.eq.jj) go to 789
s1(jj)=s1(jj)+fn*(an*pi(j)*p+bn*tau(j)*t)
s2(jj)=s2(jj)+fn*(an*tau(j)*t+bn*pi(j)*p)
789 continue
psi0=psi1
psi1=psi
apsi1=psi1
chi0=chi1
chi1=chi
xi1=cmplx(apsi1,-chi1)
n=n+1
rn=n
do 999 j=1,nang
pi1(j)=((2.*rn-1.)/(rn-1.))*amu(j)*pi(j)
pi1(j)=pi1(j)-rn*pi0(j)/(rn-1.)
999 pi0(j)=pi(j)
if (n-1-nstop) 200,300,300
300 qsca=(2./(x*x))*qsca
qext=(4./(x*x))*real(s1(1))
qback=(4./(x*x))*cabs(s1(2*nang-1))*cabs(s1(2*nang-1))
return
end
-
파장별 굴절률을 소프트웨어 입력에 용이한 형태로 변경
0.200 1.530 -0.0700000 1.530 -0.0700000 1.429 -0.0000287 1.500 -0.350
0.250 1.530 -0.0300000 1.530 -0.0300000 1.404 -0.0000015 1.620 -0.450
0.300 1.530 -0.0080000 1.530 -0.0080000 1.395 -0.0000006 1.740 -0.470
0.337 1.530 -0.0080000 1.530 -0.0050000 1.392 -0.0000001 1.750 -0.470
0.400 1.530 -0.0080000 1.530 -0.0050000 1.385 0.0000000 1.750 -0.460
0.488 1.530 -0.0080000 1.530 -0.0050000 1.382 0.0000000 1.750 -0.450
0.515 1.530 -0.0080000 1.530 -0.0050000 1.381 0.0000000 1.750 -0.450
0.550 1.530 -0.0080000 1.530 -0.0060000 1.381 0.0000000 1.750 -0.440
0.633 1.530 -0.0080000 1.530 -0.0060000 1.377 0.0000000 1.750 -0.430
0.694 1.530 -0.0080000 1.530 -0.0070000 1.376 -0.0000001 1.750 -0.430
0.860 1.520 -0.0080000 1.520 -0.0120000 1.372 -0.0000011 1.750 -0.430
1.060 1.520 -0.0080000 1.520 -0.0170000 1.367 -0.0000601 1.750 -0.440
1.300 1.460 -0.0080000 1.510 -0.0200000 1.365 -0.0001410 1.760 -0.450
1.536 1.400 -0.0080000 1.510 -0.0230000 1.359 -0.0002430 1.770 -0.460
1.800 1.330 -0.0080000 1.460 -0.0170000 1.351 -0.0003110 1.790 -0.480
2.000 1.260 -0.0080000 1.420 -0.0080000 1.347 -0.0010700 1.800 -0.490
2.250 1.220 -0.0090000 1.420 -0.0100000 1.334 -0.0003500 1.810 -0.500
2.500 1.180 -0.0090000 1.420 -0.0120000 1.309 -0.0023900 1.820 -0.510
2.700 1.180 -0.0130000 1.400 -0.0550000 1.249 -0.0156000 1.830 -0.520
3.000 1.160 -0.0120000 1.420 -0.0220000 1.439 -0.1970000 1.840 -0.540
3.200 1.220 -0.0100000 1.430 -0.0080000 1.481 -0.0669000 1.860 -0.540
3.392 1.260 -0.0130000 1.430 -0.0070000 1.439 -0.0151000 1.870 -0.550
3.500 1.280 -0.0110000 1.450 -0.0050000 1.423 -0.0071700 1.880 -0.560
3.750 1.270 -0.0110000 1.452 -0.0040000 1.398 -0.0029000 1.900 -0.570
4.000 1.260 -0.0120000 1.455 -0.0050000 1.388 -0.0036900 1.920 -0.580
4.500 1.260 -0.0140000 1.460 -0.0130000 1.377 -0.0099700 1.940 -0.590
5.000 1.250 -0.0160000 1.450 -0.0120000 1.366 -0.0095700 1.970 -0.600
5.500 1.220 -0.0210000 1.440 -0.0180000 1.333 -0.0093100 1.990 -0.610
6.000 1.150 -0.0370000 1.410 -0.0230000 1.306 -0.0796000 2.020 -0.620
6.200 1.140 -0.0390000 1.430 -0.0270000 1.431 -0.0691000 2.030 -0.625
6.500 1.130 -0.0420000 1.460 -0.0330000 1.374 -0.0294000 2.040 -0.630
7.200 1.400 -0.0550000 1.400 -0.0700000 1.343 -0.0249000 2.060 -0.650
7.900 1.150 -0.0400000 1.200 -0.0650000 1.324 -0.0279000 2.120 -0.670
8.200 1.130 -0.0740000 1.010 -0.1000000 1.324 -0.0308000 2.130 -0.680
8.500 1.300 -0.0900000 1.300 -0.2150000 1.336 -0.0336000 2.150 -0.690
8.700 1.400 -0.1000000 2.400 -0.2900000 1.366 -0.0356000 2.160 -0.690
9.000 1.700 -0.1400000 2.560 -0.3700000 1.373 -0.0365000 2.170 -0.700
9.200 1.720 -0.1500000 2.200 -0.4200000 1.356 -0.0371000 2.180 -0.700
9.500 1.730 -0.1620000 1.950 -0.1600000 1.339 -0.0368000 2.190 -0.710
9.800 1.740 -0.1620000 1.870 -0.0950000 1.324 -0.0388000 2.200 -0.715
10.000 1.750 -0.1620000 1.820 -0.0900000 1.310 -0.0406000 2.210 -0.720
10.591 1.620 -0.1200000 1.760 -0.0700000 1.271 -0.0522000 2.220 -0.730
11.000 1.620 -0.1050000 1.720 -0.0500000 1.246 -0.0731000 2.230 -0.730
11.500 1.590 -0.1000000 1.670 -0.0470000 1.227 -0.1050000 2.240 -0.740
12.500 1.510 -0.0900000 1.620 -0.0530000 1.208 -0.1900000 2.270 -0.750
13.000 1.470 -0.1000000 1.620 -0.0550000 1.221 -0.2230000 2.280 -0.760
14.000 1.520 -0.0850000 1.560 -0.0730000 1.267 -0.2710000 2.310 -0.775
14.800 1.570 -0.1000000 1.440 -0.1000000 1.307 -0.2920000 2.330 -0.790
15.000 1.570 -0.1000000 1.420 -0.2000000 1.321 -0.2970000 2.330 -0.790
16.400 1.600 -0.1000000 1.750 -0.1600000 1.407 -0.3310000 2.360 -0.810
17.200 1.630 -0.1000000 2.080 -0.2400000 1.487 -0.3410000 2.380 -0.820
18.000 1.640 -0.1150000 1.980 -0.1800000 1.525 -0.3410000 2.400 -0.825
18.500 1.640 -0.1200000 1.850 -0.1700000 1.536 -0.3390000 2.410 -0.830
20.000 1.680 -0.2200000 2.120 -0.2200000 1.560 -0.3240000 2.450 -0.850
21.300 1.770 -0.2800000 2.060 -0.2300000 1.568 -0.3180000 2.460 -0.860
22.500 1.900 -0.2800000 2.000 -0.2400000 1.579 -0.3160000 2.480 -0.870
25.000 1.970 -0.2400000 1.880 -0.2800000 1.596 -0.3130000 2.510 -0.890
27.900 1.890 -0.3200000 1.840 -0.2900000 1.612 -0.3200000 2.540 -0.910
30.000 1.800 -0.4200000 1.820 -0.3000000 1.614 -0.3200000 2.570 -0.930
35.000 1.900 -0.5000000 1.920 -0.4000000 1.597 -0.3830000 2.630 -0.970
40.000 2.100 -0.6000000 1.860 -0.5000000 1.582 -0.5610000 2.690 -1.000
-
미 산란 결과를 Origin를 이용하여 가시화
관련 자료
-
미 산란 (QSCAT.f) 소스 코드를 이용하여 4가지 입자 (Dust-like, Water soluble, Oceanic, Soot) 별 굴절률 (실수부, 허수부) 계산 및 가시화
참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com
'자기계발 > 강릉원주대 대기환경과학과' 카테고리의 다른 글
| [강릉원주대 대기환경과학과] 2017년 1학기 전선 역해석 방법 과제물 (2) (0) | 2020.03.19 |
|---|---|
| [강릉원주대 대기환경과학과] 2017년 1학기 전선 역해석 방법 과제물 (1) (0) | 2020.03.18 |
| [강릉원주대 대기환경과학과] 2016년 1학기 전선 고급 대기오염 모델링 이론/실습 및 과제물 (0) | 2020.03.18 |
| [강릉원주대 대기환경과학과] 2016년 1학기 전선 일기분석 (Ⅰ) 소개 및 과제물 (0) | 2019.12.21 |
| [강릉원주대 대기환경과학과] 2015년 2학기 전필 고급 기상 통계학 소개 및 과제물 (0) | 2019.12.20 |

