정보
-
업무명 : 2015년 2학기 전필 고급 기상 통계학 소개 및 과제물
-
작성자 : 이상호
-
작성일 : 2019-12-20
-
설 명 :
-
수정이력 :

내용
[특징]
-
고급 기상 통계학 수업에 대한 이해를 돕기위해 작성
[기능]
-
소개
-
주제별 과제물
-
자료의 특성
-
자료의 상관성
-
통계적 유의수준
-
조화 분석
-
주성분 분석
-
[사용 OS]
-
Window 10
[사용 언어]
-
Power Point 2018
-
Fortran
-
R
소개
-
안녕하세요? 기상 연구 및 웹 개발을 담당하고 있는 해솔입니다.
-
오늘은 대학원 석사 1학기에 배운 고급 기상 통계학에 대한 내용을 다루고자 합니다.
-
이 교과목은 5개 주제에 대해 15주차에 걸쳐 진행하였고 각 주제당 2주 이론 수업, 1주 개인 발표 및 토의를 진행하였습니다.
-
특히 배운 지식을 활용하여 각 주차별 발표 및 토의는 학술 논문 또는 보고서 작성 시 많은 도움이 되었습니다.
-
그에 따른 주제는 "자료의 특성, 자료의 상관성, 통계적 유의수준, 조화 분석, 주성분 분석"로서 다음과 같이 소개해드리고자 합니다.
-
추가로 각 주제에 대한 실습 자료에 대한 링크를 보내드립니다.
[R] R를 이용한 고급 기상 통계학 실습
정보 업무명 : R를 이용한 고급 기상 통계학 실습 작성자 : 이상호 작성일 : 2020-03-16 설 명 : 수정이력 : 내용 [개요] 안녕하세요? 기상 연구 및 웹 개발을 담당하고 있는 해솔입니다. 대학원 석사 1학기에 배..
shlee1990.tistory.com
주제
[자료의 특성]
-
다양한 기상 자료를 이해하기 위해서 자료에 대한 설명 (관측 지점, 관측 방법, 생산 기간)과 자료의 특성을 파악해야 합니다.
-
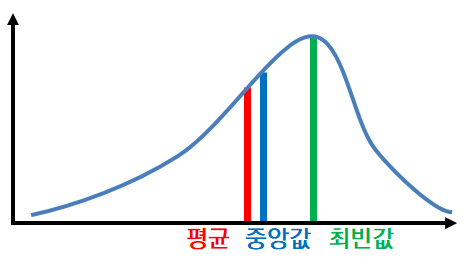
평균 (Mean)
-
일반적인 산술 평균으로 주어진 값들의 총합을 자료 개수로 나눈 값을 의미합니다.
-
-
중앙값 (Median)
-
주어진 값들을 크기 순서대로 정렬했을 때의 중앙에 위치하는 값으로서 자료의 특성에 따라 중간값이 없거나 2개 이상일 수 있습니다.
-
즉 자료의 개수가 홀수일 때 (N+1) / 2, 짝수일 때 N/2과 (N+2)/2의 산술평균으로 구합니다.
-
-
최빈값 (Mode)
-
가장 많이 관측되는 수로서 주어진 값 중에서 가장 자주 나오는 값을 의미합니다.
-
-
분산 (Variance)
-
통계에서 변량이 평균으로부터 떨어져 있는 정도를 의미하고 분산 = 0일 때 자료는 모두 평균값에 집중되어 있습니다.
-
-
표준편차 (Standard deviation)
-
자료의 분산 정도를 나타내는 수치로 분산의 양의 제곱근으로서 표준 편차가 작은 것은 평균값 주위의 분산의 정도가 작은 것을 의미합니다.
-
-
표준오차 (Standard error)
-
표준편차의 표본오차를 의미합니다.
-
-
왜도 (Skewness)
-
분포에서 중심축을 기준으로 어느 한쪽으로 치우친 정도를 의미합니다. 즉 왜도가 0이면 분포가 좌우대칭으로 볼 수 있습니다.
-
Skewness = 0 : 좌우대칭
-
Skewness > 0 : 중심축에서 왼쪽으로 치우침
-
Skewness < 0 : 중심축에서 오른쪽으로 치우침
-

-
첨도 (Kurtosis)
-
분포가 정규분포로부터 위쪽 또는 아래쪽으로 치우친 정도를 의미합니다. 즉 집중정도를 나타내는 척도입니다.
-
Kurtosis = 3 : 정규분포
-
Kurtosis > 3 : 뾰족함, 자료가 집중됨
-
Kurtosis < 3 : 평평함, 자료가 퍼짐
-

[자료의 상관성]
-
서로 다른 기상 자료의 관계를 파악하기 위해 상관 분석 및 회귀/경향 분석을 수행합니다.
-
상관계수(Correlation Coefficient)
-
두 변량 X, Y 사이의 상관관계의 정도를 나타내는 수치(계수)
-
상관계수 R은 항상 -1 ≤ R ≤ 1을 가지며 즉 R > 0은 양의 상관관계, R < 0이면 음의 상관관계, R = 0이면 상관성이 없음
-
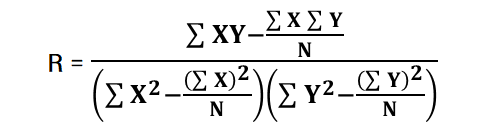
-
결정계수 (R-squared)
-
표본의 관측으로 추정한 회귀선이 실제로 관측된 표본을 어느 정도 설명해 주고 있는가? 즉 실제 관측치를 어느 정도 대표하는지 나타내는 계수
-

-
선형 회귀 분석 (Linear Regression Analysis)
-
y = Ax + B라는 방정식에서 변수 x로 y를 예측 할 수 있는 방법의 일차 방정식을 구하는 것
-
여기서 Y : 종속변수, X : 독립변수, A : 기울기(회귀계수), B : 절편(오차항)
-

-
2차 (비선형) 회귀 분석
-
y = Ax2 + Bx + c를 만족하는 2차 방정식을 구하는 것
-

[통계적 유의수준]
-
상관계수에 대한 유의성을 검증하기 위해 수행합니다.
-
통계적 유의성
-
모집단에 대한 가설이 가지는 통계적 의미
-
즉 "통계적으로 유의하다" : 어떤 실험결과가 확률적으로 봐서 단순한 우연이라고 생각되지 않을 정도로 의미가 있습니다.
-
"통계적으로 유의하지 않다" : 실험 결과가 단순한 우연일 수도 있다.
-
-
-
유의수준 (𝜶)
-
표본평균이 모평균과 같은데, 표본평균이 "모평균과 다르다"라고 선택하는 오류를 범할 허용 한계를 의미한다.
-
보통 유의수준으로 1%, 2%, 5%, 10%를 주로 사용합니다.
-
-
신뢰도 (1 - 𝜶)
-
검정하려는 귀무가설이 참인 경우, 이를 옳다고 판단하는 확률입니다.
-
귀무가설 : 설정한 가설이 진실할 확률이 극히 적어 처음부터 버릴 것이 예상되는 가설
-
대립가설 (대체가설) : 귀무가설이 기각될 때 받아들여지는 가설
-
예 : 귀무가설 : 담배는 수명에 영향을 주지 않는다 (기각), 대립가설 : 담배는 수명을 단축시킨다 (수용)
-
-
-
정규분포
-
도수분포곡선이 평균값을 중심으로 하여 좌우대칭인 종 모양을 이루는 연속 확률 분포로서 가우스 함수로 표현
-

-
표준 정규분포
-
평균이 0이고 표준편차가 1인 정규분포
-

-
가설 검정
-
귀무가설의 영역에 해당하는 함수의 넓이가 신뢰도
-
대립가설의 영역에 해당하는 함수의 넓이가 유의수준
-

-
중심극한정리 (Central limit theorem)
-
동일한 확률분포를 가진 독립 확률 변수 n개의 평균값은 n이 적당히 크다면 정규분포에 가까워진다는 정리
-
Central limit theorem - Wikipedia
In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution (informally a "bell curve") even if the original vari
en.wikipedia.org
[조화 분석]
-
시계열을 구성하는 변수를 주기항들로 구분하여 분석합니다. 즉 주화 분석 또는 스펙트럼 주기 분석이라고 합니다.
-
조화분석 (Harmonic Analysis)
-
함수 f(x)를 퓨리에 급수의 꼴로 나타내는 일로 어떤 함수 f(x)를 A0 + A1cos (x) + A2cos (2x) + … + B0 + B1 sin (x) + B2sin (2x) + … 로 전개할 때의 계수 An과 Bn을 구하는 것입니다.
-
즉 주기 함수의 퓨리에 급수전개에서 각 항의 계수를 구하는 기법이며 시계열을 구성하는 주기항들을 나누어 시간 규모에 따른 기여도를 표현한 것입니다.
-
-
Cosine and Sine functions

-
기본 주파수 (Fundamental Frequency)

-
주파수와 진폭에 따른 y 함수

-
위상차를 포함한 y 함수


-
진폭과 위상에 따른 Single Harmonic의 추정
-
삼각 함수 정의를 이용하여 식을 정리하면
-



-
등 간격으로 주어진 시계열의 경우

-
n개의 관측값으로 이루어진 시계열의 n/2개의 조화 함수

-
단 앞선 식들은 "이상 퓨리에 변환(discrete Fourier transform)"이라고 하며 식은 t=1, 2, …, (n/2-1)에만 적용됩니다.
-
따라서 가장 큰 조화 함수인 t = n/2의 경우 아래와 같은 사항을 따릅니다 (단 지금 까지의 수식들은 등 간격 시계열 한정).

[주성분 분석]
-
경험적 직교함수(Empirical Orthogonal Function, EOF)
-
주성분 분석을 말하며 통계자료를 분석함에 있어 주요 관심사 중의 하나는 자료가 가지는 변이의 내용을 파악하고 이를 해석하는 것합니다.
-
보통 변이는 일변량의 경우 그 변수의 분산으로 표현하나 다변량에서는 개별 변수의 분산 외에 서로 다른 변수들 간의 공분산 (상관계수)이 추가됩니다.
-
주성분 분석은 상관관계를 갖는 여러 개의 변수들을 선형 결합해서 주성분이라는 서로 상관관계를 갖지 않는 새로운 확률변수들을 만드는 기법입니다.
-
이 분석은 기상자료의 분석에서 변화무쌍한 역학계의 자유도를 최소화하면서 원래의 자료가 포함하고 있는 현상을 간단하게 묘사할 수 있어 많이 이용됩니다.
-
-
고유 벡터 (Eigenvector)
-
정사각행렬(n x n) A가 주어졌을 경우, 적당한 수 λ에 대하여 Ax = λx를 만족하는 영벡터 (zero vector) 이외의 벡터 x입니다. 여기서 λ를 고유값 (Eigenvalue)라고 합니다.
-
-
Ax = λx의 기하학적 의미
-
주어진 정방 행렬 A를 벡터 x에 곱하는 효과가 스칼라 λ를 x에 곱하는 것과 같은 효과를 갖게 됩니다 (상수배의 길이 늘림).
-
Ax라는 선형변환이 고유벡터 x에 가해질 때 벡터x가 방향이 아닌 크기만바뀌게 되는 변화입니다. 이 과정에서 벡터 x는 원점을 지나는 직선 위에 일치시킵니다.
-

-
예제 파일

-
주성분 분석을 위한 전처리





세부 내용
[자료의 특성]
- 자세한 내용은 URL 참조
[Fortran, Gnuplot, ShellScript] 기상 자료를 이용한 통계 분석 및 가시화
정보 업무명 : 기상 자료를 이용한 통계 분석 및 가시화 작성자 : 이상호 작성일 : 2019-08-31 설 명 : 수정이력 : 내용 [특징] 기상 자료의 특성을 파악하기 위해 통계 분석 및 가시화 도구가 필요하며 이 프로그..
shlee1990.tistory.com
[자료의 상관성]
-
추후 포스팅 예정
[통계적 유의수준]
-
추후 포스팅 예정
[조화 분석]
-
추후 포스팅 예정
[주성분 분석]
-
추후 포스팅 예정
관련 발표 자료
[자료의 특성]
[자료의 상관성]
[통계적 유의수준]
[조화 분석]
[주성분 분석]
참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com
'자기계발 > 강릉원주대 대기환경과학과' 카테고리의 다른 글
| [강릉원주대 대기환경과학과] 2016년 1학기 전선 고급 대기오염 모델링 이론/실습 및 과제물 (0) | 2020.03.18 |
|---|---|
| [강릉원주대 대기환경과학과] 2016년 1학기 전선 일기분석 (Ⅰ) 소개 및 과제물 (0) | 2019.12.21 |
| [강릉원주대 대기환경과학과] 2015년 2학기 전선 지구물리 원격탐사 소개 및 과제물 (0) | 2019.11.07 |
| [강릉원주대 대기환경과학과] 2013년 2학기 전선 대기과학전산입문 (0) | 2019.09.15 |
| [강릉원주대 대기환경과학과] 2014년 2학기 전선 대기복사학Ⅱ 과제물 (0) | 2019.09.14 |

