정보
-
업무명 : 4과목 기상통계 (도수분포와 확률)
-
작성자 : 박진만
-
작성일 : 2019-12-13
-
설 명 :
-
수정이력 :
내용
[핵심이론 01] 도수분포
-
도수분포표(Frequency (Distribution) Table)
-
각 수준의 빈도를 구하여 정리한 표로 다음 항목들을 포함한다.
-
빈도(Frequency) : 각 값이 자료에 나타난 횟수
-
상대빈도(Relative Frequency) : 총 빈도 가운데 각 값 의 빈도가 차지하는 비율
-
누적빈도(Cumulative Frequency) : 그 값까지의 빈도의 합
-
누적상대빈도(Cumulative Relative Frequency) : 그 값까지의 상대빈도의 합
-
-
-
히스토그램(Histogram)
-
양적 자료의 도수분포표를 막대로 나타낸 그림이다.
-
막대의 축척(Scale)에 의한 히스토그램의 유형
-
빈도 히스토그램은 막대의 높이가 빈도이다.
-
상대빈도(또는 백분율) 히스토그램은 막대의 높이가 상 대빈도(또는 백분율)이다. 특히 밀도 히스토그램은 막대 의 면적이 그 계급의 상대빈도이며, 이는 크기가 서로 다른 자료 집합들의 분포를 비교하기에 좋다. 백분율 히 스토그램은 막대의 면적이 그 계급의 백분율이 되도록 한 것이다. 밀도 히스토그램과 백분율 히스토그램은 세 로축의 축척만 다를 뿐 동일한 형상을 가진다. 히스토그 램은 높이가 아니라 면적으로 양을 나타낸다는 점에서 막대그래프와 다르다.
-
-
-
줄기그림(Stem Plot)
-
히스토그램과 마찬가지로 양적 자료의 전체적인 분포 형 태를 보여 주는데, 히스토그램과 달리 막대 대신에 실제 숫자를 사용한다.
-
줄기(Stem) : 각 가로줄
-
잎(Leaf) : 각 가로줄의 숫자
-
깊이(Depth) : 상향 순위와 하향 순위 중 작은 값 줄기 폭을 조절함으로써 자료의 분포 형태를 잘 나타내는 줄 기그림을 얻을 수 있다. 줄기 폭으로 가능한 값은 1, 2, 5나 이들에 \(10^{k}\)를 곱한 값들이다(여기에서 k =±1, ±2, …).
-
-
[핵심이론 02] 대표값
-
일변량(양적) 자료 분포의 몇몇 특성값(대표값, 산포도 등)들을 살펴보자.
-
기 호
-
원자료 : \(x_{1}, x_{2}, \dots, x_{n}\)
-
순서화된 자료 : \(x_{(1)}, x_{(2)}, \dots, x_{(n)}\)
-
-
-
중심 위치 측도
-
중심 위치의 측도는 대표값이라고도 부른다. 중심 위치의 측도들 가운데 평균, 중앙값, 최빈값 그리고 조화평균을 중심으로 살펴본다. 크기가 n=10인 아래의 자료를 사용한다.
-
* 자료의 예시 : (-7 -5 -4 -4 -1 2 2 2 6 9) 를 사용한다고 가정하자.
-
평균(Mean) \(\bar{x}\)
-
평균은 보통 산술평균(Arithmetic Average)이라고도 부르며, 다음과 같이 정의한다.
-
\(\bar{x}=\sum_{i} x_{i} / n\)
-
평균은 균형점, 즉 자료의 무게 중심(Balance Point, Center Of Gravity)이다.
-
평균은 제곱편차합을 최소화한다.
-
ex) 위의 자료로부터 -> \(\bar{x}=(0) / 10=0\)
-
-
중앙값(Median) \(\tilde{x}\)
-
순서화된 자료에서 가운데 위치하는 값, 즉 \(\frac{n+1}{2}\)번째 값이다.
-
\(\tilde{x}=x_{\left(\frac{n+1}{2}\right)}\)
-
만일 \(n\)이 홀수이면 중앙값은 가운데 값이고, 짝수이면 가운데 두 값들의 평균이다.
-
중앙값은 면적의 이등분점(Equal−areas 'Point)이다.
-
ex) 위의 자료에서, \(\tilde{x}=x_{\left(\frac{1+10}{2}\right)}=x_{(5.5)}=0.5\)
-
\(\left(x_{(5)}+x_{(6)}\right)=0.5(-1+2)=0.5(1)=0.5\)
-
-
최빈값(Mode) \(\check{x}\)
-
가장 빈도가 높은 값이다. 즉 최빈값은 빈도곡선에서 가장 높은 봉우리에 해당하는 값이다. 따라서 최빈값 은 여러 개가 될 수도 있다.
-
ex) 위의 자료에서, \(\check{x}=2\)
-
-
절단평균(Trimmed Mean)
-
\(p \%\) 절단평균이란 순서화된 자료의 양쪽에서 각각 \(p \%\) 에 해당하는 극단값들을 잘라낸 뒤 구한 평균을 뜻한 다. 평균이 이상값(outliers)에 민감하게 반응하는 것 을 완화시키기 위한 것이다. 체조 심사 점수는 대개 20% 절단평균이다.
-
ex) 위의 자료에서, 20% 절단평균=\((-4-4-1+2\)\(+2+2) / 6=(-3) / 6=-0.5\)
-
-
조화평균(Farmonic Mean)
-
조화평균 \(\bar{x}_{H}=\frac{n}{\sum_{i=1}^{k} \frac{1}{x_{i}}}\) 또는 \(\frac{1}{\bar{x}_{H}}=\frac{1}{n}\left(\sum_{i=1}^{k} \frac{1}{x_{i}}\right)\)
-
조화평균은 변화율(Rates Of Change)로 이루어진 자료의 평균으로 적절하다.
-
변화율 자료의 예 : 주행속도, (시간당) 생산율, 완수 (주행)시간
-
조화평균도 산술평균에 비해 이상값들의 영향을 적게 받는다. 따라서 조화평균도 오른쪽으로 꼬리를 뻗은 분포의 평균으로 유용하다.
-
-
-
상대적 위치측도
-
백분위수를 중심으로 자료 분포에서 상대적 위치를 나타내는 측도를 살펴보자
-
백분위수(Percentiles) \(P_{c}\)
-
자료를 백등분하는 값들로, 제\(c\)백분위수 \(P_{c}\)는 순서화 된 자료에서 c % 이상이 그 값보다 같거나 작고, (100- c)% 이상이 그 값보다 같거나 큰 값을 말한다.
-
-
사분위수(Quartiles) \(Q_{c}\)
-
자료를 사등분하는 세 개의 값들로, 백분위수와는 다음 관계가 있다.
-
\(Q_{1}=P_{25}, \quad Q_{2}=P_{50}=\tilde{x}, \quad Q_{3}=P_{75}\)
-
ex) 위의 자료에서, 사분위수를 각각 구하는 경우
-
\(Q_{1}=-4\),\(Q_{2}=0.5\),\(Q_{1}=2\)
-
-
[핵심이론 03] 산포도
-
자료의 (중심)위치가 파악되었다면, 자료가 중심에서 얼마나 떨어져 있는가에 관심을 가진다. 이를 산포도(Measure Of Dispersion)라 한다. 먼저 편차(Deviation)는 자료값과 어떤 중심과의 차이를 말하는데, 중심으로는 흔히 평균이 사용된다.
-
평균에서의 편차 : \(d_{i}=x_{i}-\bar{x}\)
-
평균에서의 편차는 그냥 편차라고 부른다. 산포도는 이런 편차들이 얼마나 큰가에 관한 것이다. 다음에 몇몇 산포도들을 제시하였다. 크기가 n=10인 다음의 자료를 사용한다.
-
* 자료의 예시 : (-7 -5 -4 -4 -1 2 2 2 6 9) 을 사용한다고 가정하자
-
① 범위(Range)
-
자료의 너비이다. 즉 자료의 최댓값에서 최솟값을 뺀 값이다.
-
\(R=x_{(n)}-x_{(1)}\)
-
-
② 사분위수 범위(Interquartile Range)
-
사분위수들의 너비이다.
-
\(I Q R=Q_{3}-Q_{1}\)
-
ex) 위의 자료로부터,
-
\(R=x_{(10)}-x_{(1)}=9-(-7)=16\)
\(I Q R=Q_{3}-Q_{1}=2-(-4)=6\)
-
-
③ 분산(Variance)
-
분산은 편차제곱들의 평균이다.
-
㉠ 표본분산(Sample Variance)
-
\(s^{2}=\sum\left(x_{i}-\bar{x}\right)^{2} /(n-1)=\sum\left(x_{i}^{2}-n \bar{x}^{2}\right) /(n-1)\)
-
표본분산 \(s^{2}\)의 정의에서 분모 (n-1)은 자유도 (Degrees Of Freedom, DF) 이다.
-
이는 (분자인 제곱합 항에 사용된 편차들의 정보량-자유로운 차원의 수) 를 나타낸다.
-
-
-
④ 표준편차(Standard Deviation)
-
표준편차는 분산의 단위를 자료의 측정 단위로 환원시키기 위해 분산에 양의 제곱근을 취한 것이다.
-
㉠ 표본표준편차(Sample Standard Deviation)
-
\(s=\sqrt{s^{2}}\)
-
-
-
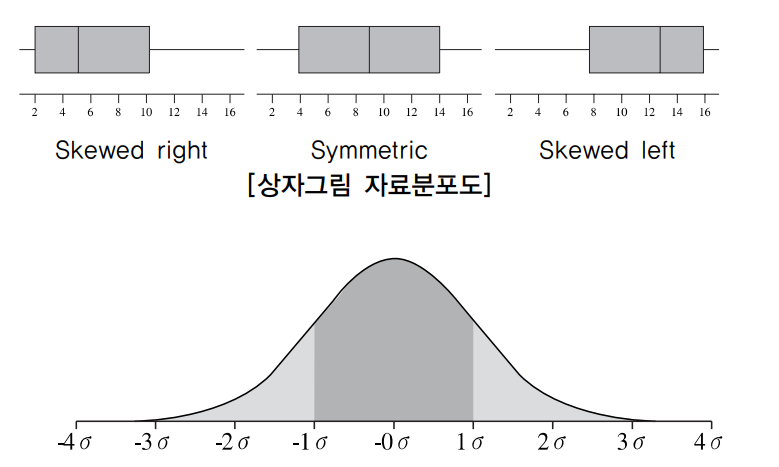
⑤ 상자그림(Boxplot)
-
사분위수들 그리고 양쪽 끝 값들 (\(x_{(1)}, Q_{1}, \tilde{x}, Q_{3}, x_{(n)}\)) 을 묶어서 다음과 같이 상자와 수염으로 나타냄으로써 자료 분포의 특징을 시각적으로 파악할 수 있다.
-
참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com
'자기계발 > 자격증' 카테고리의 다른 글
| [자격증] 기상감정기사 필기 : 4과목 기상통계 (가설검정과 추정) (0) | 2019.12.13 |
|---|---|
| [자격증] 기상감정기사 필기 : 4과목 기상통계 (확률분포) (0) | 2019.12.13 |
| [자격증] 기상감정기사 필기 : 3과목 일기해석 (위험기상과 기상요소 분석) (0) | 2019.12.13 |
| [자격증] 기상감정기사 필기 : 3과목 일기해석 (원격탐사 자료) (0) | 2019.12.13 |
| [자격증] 기상감정기사 필기 : 3과목 일기해석 (수치일기도) (0) | 2019.12.13 |

