정보
-
업무명 : 기상기사 핵심이론 소개
-
작성자 : 박진만
-
작성일 : 2019-12-07
-
설 명 :
-
수정이력 :
내용
[핵심이론 01] 포화수증기압과 Clausius-Clapeyron 방정식
-
포화수증기압의 정의
-
일정한 온도에서 수증기의 압력이 어떤 일정한 값에 도달 하면 액체와 수증기는 평형상태가 된다. 이와 같이 평형이 되었을 때의 압력이 그 온도에서 수증기가 액체와 같이 존재할 수 있는 최대한의 압력이며 이때의 수증기를 포화 되었다고 말하고, 이 포화 수증기 압력을 그 온도에서의 포화수증기압이라고 한다.
-
-
Clausius-Clapeyron 방정식(C-C 방정식)
-
엔트로피 개념을 근거로 포화수증기압과 상변화에 따른 잠열을 연관시킴으로써 다음과 같은 C-C 방정식을 얻 을 수 있다.
-
\(\frac{d e_{s}}{d T}=\frac{L_{w v}}{T\left(\alpha_{v}-\alpha_{w}\right)} \cdots\) Clausius-Clapeyron Equation
-
(w, v는 각각 물과 수증기)
-
즉, 절대온도에 대한 포화수증기압의 변화율은 잠열에 비례하고 온도에 반비례한다.
-
-
C-C 방정식을 이용한 포화수증기압 식 유도
-
C-C 방정식에서 \(\alpha_{v} \gg \alpha_{w}\) 이고 포화상태의 수증기에 대해서는 \(\alpha_{v}=R_{v} T / e_{s}\) 임을 고려
-
\(\frac{d e_{s}}{d T}=\frac{e_{s}}{T^{2}}\left(\frac{L_{w v}}{R_{v}}\right) \leftrightarrow \int_{e_{s}, 0}^{e} \frac{d e_{s}}{e_{s}}=\frac{L_{w v}}{R_{v}} \int_{T_{0}}^{T} \frac{d T}{T^{2}}\)
-
\(\begin{array}{rl}{\Rightarrow e_{s}(T)=e_{s, 0}} & {\exp \left[\frac{L_{u v}}{R_{v}}\left(\frac{1}{T_{0}}-\frac{1}{T}\right)\right]} \\ {} & {\leftrightarrow e_{s}(T)=6.112 \exp \left(\frac{17.67 T}{T+243.5}\right)}\end{array}\)
-
포화수증기압은 온도만의 함수임을 나타낸다.
-
-
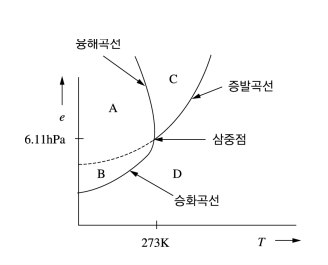
\(\mathrm{T}-\mathrm{e}_{\mathrm{s}}\) (온도-포화수증기압) Phase Diagram
-
A : 얼음 only, B : 과냉각 수적, C : 물 only, D : 수증기 only
-
과냉각 수적의 포화수증기압\(\left(e_{s}\right)\)이 같은 온도의 얼 음 포화수증기압\(\left(e_{s}\right)\) 보다 더 크다.
-
승화곡선이 증발곡선보다 더 가파르다.
-
위 곡선의 기울기를 나타내는 식이 C-C 방정식이다.
-
-
[핵심이론 02] 포화공기의 단열과정
-
습윤(건조공기+수증기) 비포화 공기의 경우, 건조단열과정 을 따르지만 수증기의 응결이 일어날 경우 응결에 따른 잠열의 방출로 건조단열과정과 차이가 난다.
-
습윤단열과정(또는 포화단열과정)
-
응결 물질이 계속 머물고 있는 경우, 그 공기덩이는 항상 같은 물질로 이루어져 있으며 가역적임
-
상변화에 따른 잠열 방출은 건조공기, 수증기, 응결 물질이 열을 가하게 됨
-
외부에서는 열이 들어오지 않기 때문에(비록 잠열로 공기 내부의 온도는 변하지만) 이 과정을 습윤단열과 정 또는 포화단열과정이라고 함 ※ 포화단열팽창과정에서 상대습도는 보존된다.
-
-
위단열과정
-
응결 물질이 생성되는 즉시 그 공기덩이로부터 낙하하 여 빠져나가는 경우, 구성 물질과 질량의 변화가 있으며 비가역적임
-
이 경우 공기덩이는 건조단열적으로 온도가 증가. 이것 은 상승할 때의 냉각률과는 다름
-
응결하여 낙하되는 물방울이 열을 가지고 가버리기 때 문에 엄밀히 단열적이 아님. 따라서 이러한 과정을 “Pseudo-adiabatic Process”(위단열과정)이라고 함
-
위단열 팽창인 경우, 온위는 보존되지 않고 증가(잠열 방출로 인함)
-
습윤단열과정인 경우 온위(θ)는 보존되지 않으며, 건조 단열과정인 경우 θ는 보존된다.
-
[핵심이론 03] 습도변수
-
수증기압 (e) : 대기의 전 압력인 대기압 중에서 수증기가 기여하고 있는 분압
-
\(e=\frac{R_{v} T}{\alpha_{v}}(\mathrm{hPa})\)
-
여기서 수증기가 들어갈 수 있는 한계를 포화수증기압 \(e_{s}(T)\)라고 한다.
-
-
절대습도(\(\rho_{v}\) ) : 단위 부피(\(\mathrm{m}^{3}\))당 수증기의 질량(g)으로 수증기 밀도로 나타낼 수 있다.
-
\(\rho_{v}=\frac{M_{v}}{V}=\frac{e}{R_{v} T}\left(\mathrm{g} / \mathrm{m}^{3}\right)\)
-
-
혼합비(w) : 건조공기 1kg(단위 질량) 속에 포함된 수증기 의 질량(g)
-
\(w=\frac{M_{v}}{M_{d}}=\frac{\rho_{v}}{\rho_{d}}=\varepsilon \frac{e}{p-e} \approx \varepsilon \frac{e}{p}(\mathrm{g} / \mathrm{kg})\)
-
-
비습(q) : 습윤공기 1kg 속에 포함된 수증기의 질량(g)
-
\(q=\frac{M_{v}}{M_{d}+M_{v}}=\frac{\rho_{v}}{\rho_{d}+\rho_{v}} \approx \varepsilon \frac{e}{p}(\mathrm{g} / \mathrm{kg})\)
\(\Rightarrow q=\frac{w}{1+w}\)
-
-
상대습도(RH) : 어떤 주어진 체적의 실제 공기가 포함하 고 있는 수증기의 양과 그 공기가 포화되었을 때 포함하고 있는 수증기의 양과의 비를 뜻한다.
-
\(R H=\frac{w}{w_{s}}=\frac{e}{e_{s}}=\frac{q}{q_{s}}(\%)\)
-
-
가온도(\(T_{v}\)) : 습윤공기를 건조공기처럼 다루기 위한 가상 적인 온도이다.
-
\(T_{v}=T\left(\frac{1+w / \varepsilon}{1+\varepsilon}\right)=T\left(\frac{1+1.609 w}{1+w}\right):\)
\(\varepsilon=m_{v} / m_{d}=0.622\)
-
-
노점온도(\(T_{d}\)) : 습윤공기를 압력(P)과 혼합비(w)가 일 정한 상태에서 포화에 이르기 위해 도달되어야 할 온도 이다. (ex : 겨울철 복사냉각에 의해 이슬이 생긴다.)
-
상승응결고도(LCL) : 불포화 공기가 상승하면서 건조단 열팽창을 하여 포화되어 응결이 이루어지는 고도이다.
-
대류응결고도(CCL) : 지상의 공기덩이가 가열로 인하여 에너지를 얻어 자력으로 상승하여 포화에 이르는 고도이다.
-
습구온도(\(T_{w}\)) : 해당 공기덩이가 단열적으로 포화되도록 냉각된 후 포화단열 과정을 거쳐 본래의 기압으로 단열적 으로 압축되어 나타나는 온도이다.
-
습구온위(\(\theta_{w}\))
-
\(T_{w}\)를 습윤단열적으로 1,000hPa 까지 끌어내렸을 때 의 온도이다.
-
상당온위(\(\theta_{e}\))와 마찬가지로 습구온위(\(\theta_{w}\))도 습윤과 건조단열과정 동안에 보존된다.
-
-
상당온도(\(T_{e}\))
-
주어진 공기를 단열적으로 상승시키면서 그 공기 중에 포함되어 있는 모든 수증기를 완전히 응결시켜 탈락시킨 후 원래의 기압고도까지 단열적으로 하강시켰을 경 우에 나타낼 온도이다.
-
\(T_{e}=T \exp \left\{\frac{L w_{s}}{C_{p} T}\right\}\) : 단열과정 동안에 보존되지 않는다.
-
-
상당온위(\(\theta_{e}\))
-
\(T_{e}\)를 건조단열적으로 1,000hPa 까지 이동하였을 때의 온도이다.
-
\(\theta_{e}=\theta \exp \left\{\frac{L w_{s}}{C_{p} T}\right\}\) : 건조단열과정과 습윤단열 과정 동안에 보존된다.
-
'자기계발 > 자격증' 카테고리의 다른 글
| [자격증] 기상기사 필기 : 3과목 대기운동학 (대기운동학) (0) | 2019.12.08 |
|---|---|
| [자격증] 기상기사 필기 : 2과목 대기열역학 (대기 안정도 및 단열선도) (2) | 2019.12.08 |
| [자격증] 기상기사 필기: 2과목 대기열역학 (열역학 법칙) (0) | 2019.12.07 |
| [자격증] 기상기사 필기: 2과목 대기열역학 (대기열역학 기초) (0) | 2019.12.07 |
| [자격증] 기상기사 필기: 1과목 기상관측법 (특수관측) (0) | 2019.12.07 |

