정보
-
업무명 : 선형 회귀 : 점수검정
-
작성자 : 박진만
-
작성일 : 2020-04-19
-
설 명 :
-
수정이력 :
내용
[개요]

[특징]
-
통계이론 설명
[활용 자료]
-
없음
[자료 처리 방안 및 활용 분석 기법]
-
없음
[사용법]
-
내용 참조
상세 내용
[귀무 가설과 대립 가설]
-
가설 검정은 귀무 가설을 기각 여부 통계적으로 결정하는 방법이다.
-
일반화 선형 모델에서 그 모델의 로그 가능도의 1 차 도함수는 점수로 정의되어있다.
-
관심있는 모델 매개 변수의 최대 가능도 방법 량이 유의 경우 그 최대 가능도 방법 형량을 대수 우도 함수의 1 차 도함수에 대입하면 0이되면 기대할 수 있다.
-
즉, 귀무 가설이 성립한다면 점수는 0이된다 기대할 수있다. 점수 검정은이 점을 이용한 검정이다.
-
\(\hat{\beta}\)모델의 최대 가능성 추정 점수의 귀무 가설과 대립 가설은 다음과 같이 설명 할 수 있다.

[점수 통계]
-
점수는 대수 우도 함수의 1 차 도함수로 정의되어있다.

-
다음으로 귀무 가설에 대응하는 모델 및 관심있는 모델의 최대 가능성 추정치를 각각 \(\hat{\beta}^{1}, \hat{\beta}^{0}\) 라 한다.
[점수의 기대 값과 분산 공분산 행렬 행렬]
-
점수의 기대 값과 분산 공분산 행렬은 다음과 같이 할 수 있다.

[통계 분포]
-
일반적으로 연속적인 값 t가 존재할 때, t는 정규 분포에 근사한다.
-
또한 t를 표준화하면 t는 표준 정규화에 따른다. 즉

-
이것은 아래의 식과 같다.
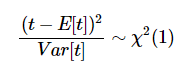
-
여기서 t가 요소 수, p가 벡터일 때, 다음과 같이 표현할 수있다. 여기서 V 는 공분산 행렬이다.

[점수 통계]
-
여기서 t 를 통계 \(\mathbf{U}(\hat{\beta})\)로 대체하고 귀무 가설에서 \(E[\mathbf{U}(\hat{\beta})]=0\) 이라면 다음 관계가 얻어진다.

-
점수 검정에서는 왼쪽이 자유도 p 카이 제곱 분포에 따라 검정을 실시한다.
참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com
본 블로그는 파트너스 활동을 통해 일정액의 수수료를 제공받을 수 있음
'통계 이론' 카테고리의 다른 글
| [통계] 업비트 비트코인-이더리움 실시간 매수-매도량 감시 프로그램 (모니터링) (0) | 2022.10.11 |
|---|---|
| [통계이론] 선형회귀 : Wald 검정 (0) | 2020.05.30 |
| [통계 이론] 선형 회귀 : 우도비검정 (2) | 2020.04.20 |
| [통계 이론] 선형 회귀 : 로그 우도 함수의 최대 우도 (가능도) 추정 (0) | 2020.04.19 |
| [통계 이론] 선형 회귀 : 오차구조 (error structure), 연결 함수 (link function), 선형 예측 (linar predictor) (0) | 2020.04.19 |

