[통계 이론] 선형 회귀 : 로그 우도 함수의 최대 우도 (가능도) 추정
정보
-
업무명 : 선형 회귀 : 로그 우도 함수의 최대 우도 (가능도) 추정
-
작성자 : 박진만
-
작성일 : 2020-04-19
-
설 명 :
-
수정이력 :
내용
[개요]

[특징]
-
통계이론 설명
[활용 자료]
-
없음
[자료 처리 방안 및 활용 분석 기법]
-
없음
[사용법]
-
내용 참조
상세 내용
[로그 우도 함수의 최대 가능도 추정]
-
일반화 선형 모형으로 랜덤 변수 Y를 모델링 할 때 매개 변수가 β이고, 디자인 행렬이 X이고 링크 함수가 g 인 경우 모델은 아래의 식과 같이 쓰여질 수 있다.
-
이 때, 일반화 선형 모델에 내장 된 매개 변수 β으 최대 가능도를 추정하는 방법을 보여준다.

[일반화 선형 모형의 로그 가능도]
-
랜덤 변수 Y의 밀도 함수는 다음 식과 같이 지수 분포 집합으로 표현 될 수 있다고 가정한다.

-
여기서 밀도 함수 f (Y; θ)의 경우 그 가능도 L (θ Y) = f (Y; θ)도 유사한 식으로 나타낼 수 있으며, 이 때 로그 우도 함수는 다음과 같이 쓰여질 수 있다.

-
이제, n 개의 랜덤 변수 y1, ..., yn이 있다면, 현재 로그 우도 함수는 다음과 같이 쓸 수 있다.
-
이 경우 최적의 파라미터 β를 찾기 위해,이 로그 우도 함수를 최대화하는 β를 찾을 수 있다.

-
로그 우도 함수의 2 차 미분은 음수 값을 취하므로, 로그 우도 함수의 최대 값은 1 차 미분이 0인 경우가 될 것이다.

-
여기서 Newton-Raphson 방법은 로그 우도 함수의 1 차 미분이 0 인 β를 찾는 데 사용된다.
-
Newton-Raphson 방법을 사용하려면 1 차 미분뿐만 아니라 2 차 미분 역시 필요하다.
-
즉 여기에서 먼저 로그 우도 함수의 1 차 및 2 차 미분을 찾아야 한다.
[최대 가능도 추정량 (로그 가능도의 1 차 미분)]
-
로그 가능도의 1 차 미분은 다음과 같이 쓸 수 있다.
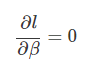
-
먼저, 좌변의 로그 우도 함수의 미분을 쉽게 계산할 수 있도록 공식 변환을 하여야 한다.
-
연쇄미분으로 인해, \(\frac{\partial l}{\partial \beta}\) 는 아래와 같이 세 가지 부분으로 분해 될 수 있다.

-
여기서 첫번째 항에 대해서는 로그 가능도를 θi 로 미분하면 해를 구할 수 있다.

-
여기서 두 번째 항에 대해서는 \(\frac{A^{\prime}(\theta)}{\eta^{\prime}(\theta)}=\mu\)의 관계를 사용하여 해를 구할 수 있다.

-
세 번째 항의 경우 링크 함수의 양변을 β로 미분 하여야 한다.
-
여기서 디자인 행렬 X 의 i 번째 줄의 행 벡터에 대해 미분한다.

-
결과적으로 로그 가능도를 β로 미분 한 식은 아래와 같이 쓰여질 수 있다.
-
로그 가능도를 미분 한 cost의 결과는 cost 함수로 불린다. cost 함수는 일반적으로 기호 U로 나타내는 경우가 많다.

[로그 가능도의 2차 미분]
-
\(\frac{\partial^{2} l}{\partial \beta \partial \beta^{T}} \int f(y ; \beta) d y=1\)

-
따라서

-
우변은 로그 가능도를 β로 미분 한 것이므로, 로그 가능도의 1차 미분에서 얻어진 결과를 대입하여 정리 할 수 있다.

-
그리고 wi는

-
또한 W 를 w로 이루어진 행렬로 나타내면

-
로그 우도 함수의 첫 번째 미분은 cosgt 함수라고하며, 점수 함수의 분산은 피셔 정보라고 부른다.
-
즉 p 개의 파라미터가 있는 경우, 각각의 p 개의 파라미터에 대한 피셔 정보량이 획득된다.
-
이러한 피셔 정보량을 p × p 양의 명확한 대칭 행렬로 표현하는 행렬을 피셔 정보 행렬이라고 한다.
-
피셔 정보 행렬은 I 또는 F로 쓰여진다.

-
여기서 얻은 \(\mathbf{X}^{\top} \mathbf{W} \mathbf{X}\)는 로그 우도 함수의 2 차 미분 값이다.
-
이제 1 차 및 2 차 미분의 예상 값을 얻었으므로 로그 가능성 함수를 최대화하는 β는 Newton-Raphson 방법 (IRLS 알고리즘)을 사용하여 얻을 수 있다.
[Newton-Raphson 방법]
-
구하고자 하는 것은 \(\frac{\partial l}{\partial \beta}=U=0\) 이다. 따라서 로그 가능도의 1 차 미분을 제 2 항에 대해서 테일러 급수 전개를 시행한다.

-
이를 정리하면 다음과 같다.

-
Newton-Raphson 방법은 이러한 표현을 반복적으로 사용하여 최적의 β를 계산한다.

참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com
본 블로그는 파트너스 활동을 통해 일정액의 수수료를 제공받을 수 있음