[Fortran] 포트란 Random 함수를 이용한 정규 분포 가시화
정보
-
업무명 : 포트란 Random 함수를 이용한 정규 분포 가시화
-
작성자 : 이상호
-
작성일 : 2020-01-29
-
설 명 :
-
수정이력 :
내용
[개요]
-
안녕하세요? 웹 개발 및 연구 개발을 담당하고 있는 해솔입니다.
-
기상 자료의 특성을 파악하기 위해서 자료의 빈도분포와 정규 분포를 비교 분석하는 것은 비일비재합니다.
-
일반적으로 통계 프로그래밍 언어 R을 통해 정규 분포를 구현 및 가시화하나 빅 데이터일수록 오랜 시간 소요되는 단점이 있습니다.
-
따라서 고속 계산이 가능한 포트란 (Fortran)에서 Random 함수 (random_seed, random_number)을 이용하여 정규 분포 생성을 소개드리고자 합니다.
[특징]
-
기상 빅 데이터를 분석하기 위해서 Random 함수 사용 기술이 요구되며 이 프로그램은 이러한 목적을 달성하기 위한 소프트웨어
[기능]
-
Random 함수를 통해 정규분포 생성
-
Gnuplot을 이용한 빈도분포 가시화
[활용 자료]
-
없음
[자료 처리 방안 및 활용 분석 기법]
-
없음
[사용법]
-
작업 환경 구축
-
소스 코드 실행 (csh Histogram_Using_Gnuplot.csh)
-
Fortran 컴파일/실행 (ifort *.f90 ; ./a.out)
-
Gnuplot 가시화
-
-
가시화 결과 확인
[사용 OS]
-
Linux (CentOS v7.0)
-
VMware Workstation Pro v15.5
[사용 언어]
-
Fortran (ifort v19.1.0.166)
-
Gnuplot v5.2
-
Shell Script (csh)
소스 코드
[명세]
-
Fortran
-
반복 횟수 (1,000,000 번) 및 평균/표준편차 (0 / 2)에 대한 정규 분포 생성
-
이 과정에서 "ran" 함수를 통해 0-1의 랜덤값 생성하고 "normal" 함수 호출
-
그 결과를 "out.txt" 출력
-
module ran_mod
implicit none
! ran return a uniform random number between 0-1
! norma return a normal distribution
contains
! returns random number between 0-1
function ran()
implicit none
integer, save :: flag = 0
double precision :: ran
if (flag == 0) then
call random_seed()
flag = 1
endif
! built in fortran 90 random number function
call random_number(ran)
end function ran
function normal(mean,sigma)
implicit none
integer :: flag
double precision, parameter :: pi = 3.141592653589793239
double precision :: u1, u2, y1, y2, normal, mean, sigma
save flag
data flag /0/
u1 = ran()
u2 = ran()
if (flag == 0) then
! y1 = sqrt(-2.0d0 * log(u1)) * cos(2.0d0 * pi * u2)
! normal = mean + sigma * y1
normal = u1
flag = 1
else
! y2 = sqrt(-2.0d0 * log(u1)) * sin(2.0d0 * pi * u2)
! normal = mean + sigma * y2
normal = u2
flag = 0
endif
end function normal
end module ran_mod
program Random_Sample_Template
use ran_mod
implicit none
integer, parameter :: N = 1000000
real(8) :: arrVal(N)
integer :: iCount
open(12, file = "out.txt")
do iCount = 1 , N
arrVal(iCount) = normal(0.0D0, 2.0D0)
write(12, *) arrVal(iCount)
end do
close(12)
end program Random_Sample_Template
-
Gnuplot
-
글꼴 및 크기 지정
-
출력 그림 설정
-
x축, y축, 범례 설정
-
0.5 간격에 대한 빈도분포 가시화
-
set terminal post enhanced color font "Time-Roman, 20" background rgb "white"
set output "${iNumber}.gif"
set grid
set key noopaque
set key top right
set xlabel "Sample Distribution"
set ylabel ""
set title "Central Limit Theorem : Number of Sample = ${sNumber}"
binwidth = 0.5
bin(x, width) = width * floor(x / width) + width / 2.0
plot 'out.txt' using (bin(\$1, binwidth)):(1.0) t "" smooth freq with boxes
-
Shell Script (csh)
-
반복 횟수 (arrNumber)에 대해 반복문 수행
-
Random_Sample_Template.f90에서 "%iNumber"을 "iNumber"로 치환
-
ifort를 통해 컴파일 및 실행
-
출력 결과 ("out.txt")에 대해 Gnuplot 가시화 및 그림 저장
-
#!/bin/csh
set arrNumber = (100 10000 1000000 100000000)
foreach iNumber ($arrNumber)
set sNumber = `printf "%'d" ${iNumber}`
cat Random_Sample_Template.f90 | \
sed -e "s/%iNumber/${iNumber}/g" > Random_Sample.f90
ifort Random_Sample.f90 ; ./a.out
gnuplot << EOF
set terminal post enhanced color font "Time-Roman, 20" background rgb "white"
set output "${iNumber}.gif"
set grid
set key noopaque
set key top right
set xlabel "Sample Distribution"
set ylabel ""
set title "Central Limit Theorem : Number of Sample = ${sNumber}"
binwidth = 0.5
bin(x, width) = width * floor(x / width) + width / 2.0
plot 'out.txt' using (bin(\$1, binwidth)):(1.0) t "" smooth freq with boxes
EOF
mogrify -rotate 90 ${iNumber}.gif
mv -f ${iNumber}.gif FIG/.
end
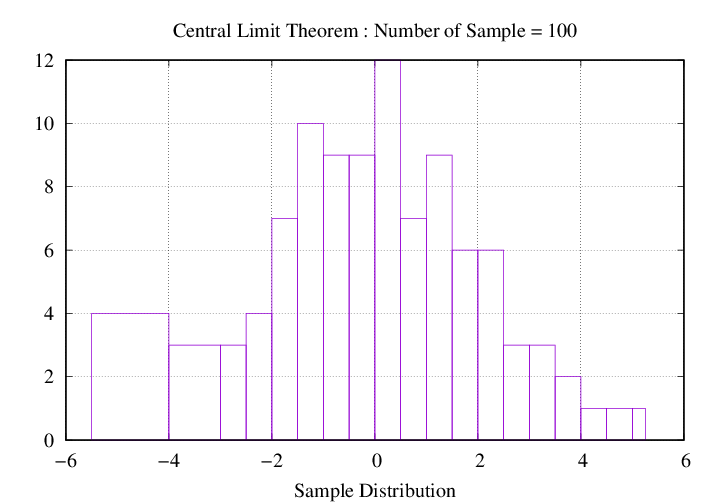
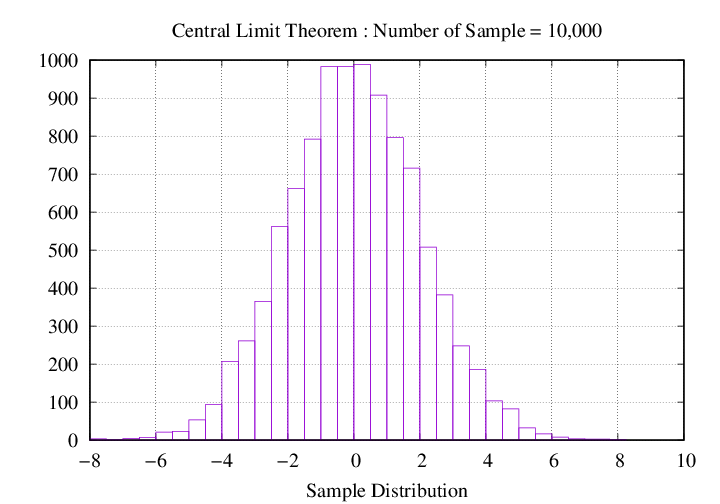
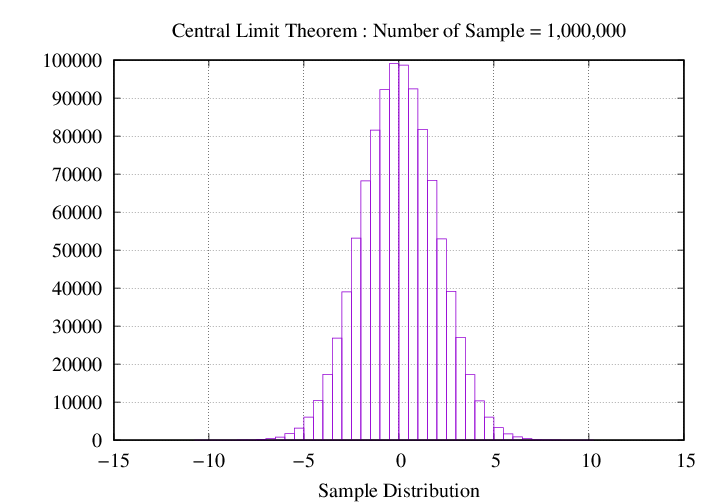
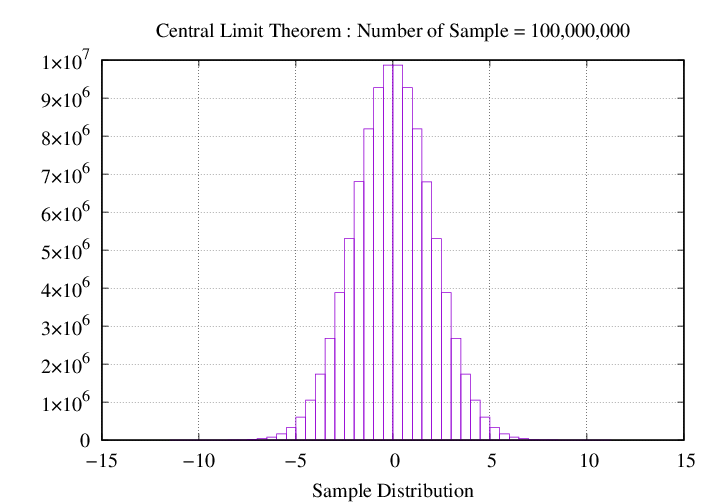
참고 문헌
[논문]
- 없음
[보고서]
- 없음
[URL]
- 없음
문의사항
[기상학/프로그래밍 언어]
- sangho.lee.1990@gmail.com
[해양학/천문학/빅데이터]
- saimang0804@gmail.com